(C1) Алгебраические выражения, уравнения, неравенства и их системы
Задание 3771
Найдите сумму целых отрицательных решений неравенства $$\frac{x^{2} + 2x + 10}{x - 2} \ge -3$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\frac{x^{2}+2x+10}{x-2} \geq -3\Leftrightarrow$$$$\frac{x^{2}+2x+10}{x-2}+3 \geq 0\Leftrightarrow$$$$\frac{x^{2}+2x+10}{x-2}+\frac{3(x-2)}{x-2} \geq 0\Leftrightarrow$$$$\frac{x^{2}+2x+10+3x-6}{x-2} \geq 0\Leftrightarrow$$$$\frac{x^{2}+5x+4}{x-2} \geq 0$$
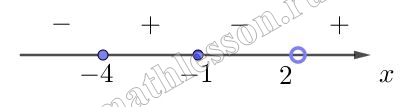
Найдем при каких значениях x числитель дроби равен нулю и отметим эти значения (закрашенные, так как неравенство нестрогое), а так же значение, когда знаменатель равен нулю (пустое, так как мы должны исключить данное значение из ОДЗ) на координатной прямой и расставим знаки значений, которые принимает дробь на полученных промежутках:
Нам необходимо выбрать те промежутки, где дробь принимает положительные значения, а так же из данных промежутков найти сумму всех целых отрицательных значений: $$-4+(-3)+(-2)+(-1)=-10$$
Задание 4672
Один из корней уравнения $$5x^2 - 2x + 3p = 0$$ равен $$1$$. Найдите второй корень.
Подставим $$x=1$$:
$$5\cdot1-2\cdot1+3p=0$$; $$3p+3=0$$; $$p=-1$$ Подставим и найдем 2 корень: $$5x^{2}-2x-3=0$$; $$D=4+60=64$$; $$x_{1}=\frac{2+8}{10}=1$$; $$x_{2}=\frac{2-8}{10}=-0,6$$
Задание 795
При каких целых значениях $$n$$ выражение $$\frac{2n - 3}{n + 1}$$ является целым числом?
$$\frac{2n-3}{n+1}=\frac{2n+2-2-3}{n+1}=\frac{2n+2}{n+1}-\frac{5}{n+1}\Leftrightarrow 2-\frac{5}{n+1}$$
Так как $$n\in Z,$$ то $$\frac{5}{n+1}$$ должно тоже быть целым, чтобы $$\frac{2n-3}{n+1}\in Z.$$
Тогда $$n+1$$ делит нацело 5:
$$\left[\begin{matrix} n+1=\pm1\\ n+1=\pm5 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} n=0;-2\\ n=-6;4 \end{matrix}\right.$$
Задание 1422
Решите неравенство: $$(2x + 1)(x - 1) > 9$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4650
Решите неравенство: $$(4x - 6)^{2}\ge (6x - 4)^{2}$$
$$(4x-6)^{2}-(6x-4)^{2}\geq0\Leftrightarrow$$$$(4x-6-6x+4)(4x-6+6x-4)\geq0\Leftrightarrow$$$$(-2x-2)(10x-10)\geq0\Leftrightarrow$$$$-2(x+1)\cdot10(x-1)\geq0\Leftrightarrow$$$$(x+1)(x-1)\leq0$$
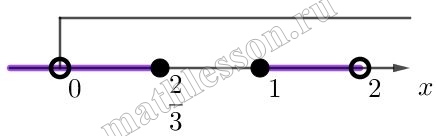
Начертим координатую прямую, отметим значения х при которых выражение $$(x+1)(x-1)$$ равно 0 и отметим знаки значений, которые принимает данное выражение на полученных промежутках:

Выберем те, в которых выражение неположительное : $$[-1; 1]$$
Задание 4651
Решите неравенство: $$(x - 7)^{2} < \sqrt{11}(x - 7)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$(x-7)^{2}-\sqrt{11}(x-7)<0$$
$$(x-7)(x-7-\sqrt{11})<0$$
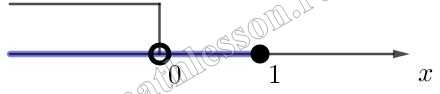
Начертим координатную прямую, отметим значения х при которых выражение $$(x-7)(x-7-\sqrt{11})$$ равно нулю и расставим знаки значений, которые принимает данное выражение на полученных промежутках:

Выберем те, в которых выражение принимает отрицательные значения: $$(7; 7+\sqrt{11})$$
Задание 4358
Решите неравенство: $$(x + 1-\sqrt{3})^2 \cdot (x - \sqrt{6} + 2) > 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$(x+1-\sqrt{3})^{2}\cdot(x-\sqrt{6}+2)>0$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}(x-\sqrt{6}+2)>0\\x+1-\sqrt{3}\neq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x>\sqrt{6}-2\\x\neq\sqrt{3}-1\end{matrix}\right.$$
Задание 3959
Решите неравенство: $$(x + 2)^3 \ge 4(x + 2)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$(x+2)^{3}-4(x+2)\geq0\Leftrightarrow$$$$(x+2)((x+2)^{2}-4)\geq0\Leftrightarrow$$$$(x+2)(x+2+2)(x+2-2)\geq0\Leftrightarrow$$$$(x+2)(x+4)x\geq0$$. То есть получили выражение $$f(x)=(x+2)(x+4)x$$
Отметим на координатной прямой в каких случаях выражение полученное равно нули, расставим знаки, которые оно принимает:
Нам необходимы те промежутки, где выражение положительное, то есть: $$x\in[-4;-2]\cup[0;+\infty)$$
Задание 4652
Решите неравенство: $$\frac{-10}{(x - 3)^{2} - 5} \ge 0$$
$$\frac{-10}{(x-3)^{2}-5}\geq0$$ $$\Leftrightarrow$$ $$(x-3)^{2}-5<0$$ $$\Leftrightarrow$$ $$(x-3-\sqrt{5})(x-3+\sqrt{5})<0$$
Отметим на координатной прямой значения х, при которых выражение $$(x-3-\sqrt{5})(x-3+\sqrt{5})$$ равно 0 и расставим знаки значений, которые принимает данное выражение на полученных промежутках:

Выберем те, в которых данное выражение принимает отрицательные значения: $$(3-\sqrt{5}; 3+\sqrt{5})$$
Задание 4546
Решите неравенство: $$\frac{-22}{x^2 - 2x -35} \le 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Числитель $$-22$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была отрицательной, знаменатель должен быть положительным: $$x^2 - 2x - 35 > 0.$$
2) Решим неравенство: $$x^2 - 2x - 35 > 0.$$ Учтём, что $$x^2 - 2x - 35 = (x-7)(x+5).$$ Нули: $$x_1 = -5;\quad x_2 = 7.$$ Отметим их на координатной прямой и расставим знаки, которые принимает выражение $$(x-7)(x+5)$$ на полученных промежутках.
Выражение положительное при: $$x \in (-\infty;\,-5) \;\cup\; (7;\,+\infty).$$
Задание 2614
Решите неравенство: $$\frac{(x - 2)(x^2 - 4) - (7 + x - x^2)(x^2 - 4)}{x^4 - 81} \ge 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


ОДЗ: $$x^{4}-81\neq0$$ $$\Rightarrow$$ $$x^{4}\neq81$$ $$\Rightarrow$$ $$x\neq\pm3$$
Решение: $$\frac{(x^{2}-4)(x-2-7-x+x^{2})}{(x^{2}-9)(x^{2}+9)}\geq0$$ $$\Leftrightarrow$$ $$\frac{(x-2)(x+2)(x^{2}-9)}{(x^{2}-9)(^{2}+9)}\geq0$$ $$\Leftrightarrow$$ $$\frac{(x-2)(x+2)}{x^{2}+9}\geq0$$ $$\Rightarrow$$ $$(x-2)(x+2)\geq0$$ $$\Rightarrow$$ $$x\in(-\infty;-2]\cup[2;+\infty)$$
С учетом ОДЗ: $$x\in(-\infty;-3)\cup(-3;-2]\cup[2;3)\cup(3;+\infty)$$
Задание 3338
Решите неравенство: $$\frac{(x+2)(x+1)}{x^2 - |x| - 2} \le -3x$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Область определения: $$x^{2}-|x|-2\neq 0\Leftrightarrow$$$$|x|\neq 2, |x|\neq -1\Leftrightarrow$$$$x\neq \pm 2$$
Раскроем модуль:
1) При $$x\geq 0 \Rightarrow$$ $$\frac{(x+2)(x+1)}{x^{2}-x-2} \leq -3x\Leftrightarrow$$ $$\frac{(x+2)(x-1)}{(x-2)(x+1)}\leq -3x\Leftrightarrow$$ $$\frac{x+2}{x-2}+3x\leq 0$$
Рассматриваем числитель дроби, чтобы разбить его на множители: $$3x^{2}-5x+2=0$$
$$D=25-24=1$$
$$x_{1}=\frac{5+1}{6}=1$$
$$x_{2}=\frac{5-1}{6}=\frac{2}{3}$$
Следовательно,$$\frac{(x-\frac{2}{3})(x+1)}{x-2}\leq 0$$
2) При $$x<0 \Rightarrow$$$$\frac{(x+2)(x+1)}{x^{2}+x-2}\leq -3x\Leftrightarrow$$ $$\frac{(x+2)(x+1)}{(x+2)(x-1)}+3x\leq 0\Leftrightarrow$$$$\frac{x+1}{x-1}+3x\leq 0\Leftrightarrow$$ $$\frac{x+1+3x^{2}-3x}{x-1}\leq 0\Leftrightarrow$$ $$\frac{3x^{2}-2x+1}{x-1}\leq 0$$
Рассмотрим числитель полученной дроби:
$$3x^{2}-2x+1=0$$
$$D=4-12<0$$
Следовательно, числитель данной дроби всегда положителен и не влияет на знак неравенства: $$\frac{1}{x-1}\leq 0$$
С учетом обрасти опредеделения:
$$x \in (-\infty ;-2)\cup(-2;\frac{2}{3})\cup [1; 2)$$