(C5) Геометрическая задача на доказательство
Задание 1296
Биссектрисы углов $$C$$ и $$D$$ трапеции $$ABCD$$ пересекаются в точке $$P$$, лежащей на стороне $$AB$$. Докажите, что точка $$P$$ равноудалена от прямых $$BC$$, $$CD$$ и $$AD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3288
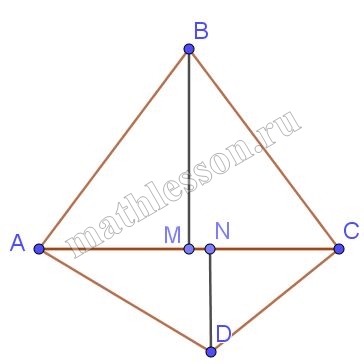
В выпуклом четырёхугольнике $$ABCD$$ противоположные углы $$A$$ и $$C$$ прямые. На диагональ $$AC$$ опущены перпендикуляры $$BM$$ и $$DN$$. Докажите, что $$CM = NA$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$\angle ABM=\alpha$$, тогда из $$\Delta ABM: \angle BAM=90-\alpha$$ , тогда $$\angle MAD=\alpha$$ и из $$\Delta ADH:$$$$\angle ADN =90-\alpha \Rightarrow$$ $$\Delta ABM\sim \Delta AND$$, тогда : $$\frac{DH}{AM}=\frac{AN}{BM}\Rightarrow$$ $$DN*BM=AM*AN(1)$$
2) Аналогично $$\Delta BMC\sim \Delta CHD$$ и $$\frac{DH}{CM}=\frac{NC}{BM}\Rightarrow$$ $$DN*BM=CM*NC(2)$$
3) С учетом (1) и (2): $$AM *AN=CM*NC$$ или $$AM(AM+MN)=CN(CN+MN)\Leftrightarrow$$ $$AM^{2}+AM*MN=CN^{2}+CN*MN\Leftrightarrow$$ $$AM^{2}-CN^{2}+AM*MN-CN*MN=0\Leftrightarrow$$ $$(AM-CN)(AM+CN)+MN(AM-CN)=0\Leftrightarrow$$ $$(AM-CN)(AM+CN+MN)=0$$. $$AM+CN+MN>0$$ всегда, следовательно, $$AM-CN=0$$ или $$AM=CN$$
Задание 4190
В выпуклом четырехугольнике $$ABCD$$ точки $$K$$, $$M$$, $$P$$, $$E$$ – середины сторон $$AB$$, $$BC$$, $$CD$$ и $$DA$$ соответственно. Докажите, что площадь четырехугольника $$KMPE$$ равна половине площади четырехугольника $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) из $$\bigtriangleup ABC$$: $$KM\parallel AC$$ (км - средняя линия)
аналогично: $$KE\parallel DB\parallel MP$$; $$KM\parallel AC\parallel EP$$ и $$EP=KM$$; $$EK=PC$$
2) $$S_{ABD}+S_{DBC}=S_{ABC}+S_{ADC}=S_{ABCD}=S$$
$$\left.\begin{matrix}S_{AKE}=\frac{1}{4}S_{ABD}\\S_{KCP}=\frac{1}{4}S_{DBC}\\S_{KBM}=\frac{1}{4}S_{ACB}\\S_{EDP}=\frac{1}{4}S_{ADC}\end{matrix}\right\}$$ $$\Rightarrow$$
$$\frac{1}{4}(S_{ABD}+S_{DBC})+\frac{1}{4}(S_{ACB}+S_{ADC})=\frac{1}{4}S+\frac{1}{4}S=\frac{1}{2}S$$ $$\Rightarrow$$
$$S_{EKMP}=S-\frac{1}{2}S=\frac{1}{2}S$$
Задание 775
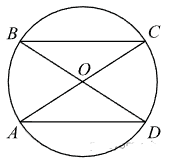
В окружности через середину $$O$$ хорды $$BD$$ проведена хорда $$AC$$ так, что дуги $$AB$$ и $$CD$$ равны. Докажите, что $$O$$ — середина хорды $$AC$$.
Задание 2555
В остроугольном треугольнике $$ABC$$ точки $$A$$, $$C$$, центр описанной окружности $$O$$ и центр вписанной окружности $$I$$ лежат на одной окружности. Докажите, что угол $$ABC$$ равен $$60^{\circ}$$ .
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1776
В остроугольном треугольнике $$ABC$$ угол $$B$$ равен $$60^{\circ}$$. Докажите, что точки $$A$$, $$C$$, центр описанной окружности треугольника $$ABC$$ и точка пересечения высот треугольника $$ABC$$ лежат на одной окружности.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 981
В параллелограмме $$ABCD$$ проведены высоты $$BE$$ и $$BF$$ к сторонам $$AD$$ и $$CD$$ соответственно. Докажите, что треугольник $$ABE$$ подобен треугольнику $$CBF$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


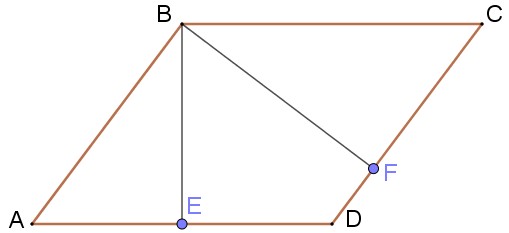
- $$BE\perp AD \Rightarrow \angle BEA=90^\circ$$
- $$BF\perp DC \Rightarrow \angle BFC=90^\circ\Rightarrow$$ $$\angle BEA\angle BFC$$
- $$ABCD$$ - параллелограмм, тогда $$\angle BAE=\angle BCF$$
- $$\triangle ABE \sim \triangle CBF$$ по двум углам.
Задание 1051
В параллелограмме $$ABCD$$ точка $$M$$ — середина стороны $$CD$$ . Известно, что $$MA=MB$$. Докажите, что данный параллелограмм — прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!