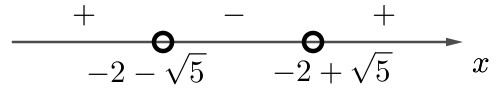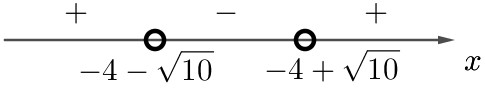Задание 4652
Задание 4652
Решите неравенство: $$\frac{-10}{(x - 3)^{2} - 5} \ge 0$$
$$\frac{-10}{(x-3)^{2}-5}\geq0$$ $$\Leftrightarrow$$ $$(x-3)^{2}-5<0$$ $$\Leftrightarrow$$ $$(x-3-\sqrt{5})(x-3+\sqrt{5})<0$$
Отметим на координатной прямой значения х, при которых выражение $$(x-3-\sqrt{5})(x-3+\sqrt{5})$$ равно 0 и расставим знаки значений, которые принимает данное выражение на полученных промежутках:
Выберем те, в которых данное выражение принимает отрицательные значения: $$(3-\sqrt{5}; 3+\sqrt{5})$$
Аналоги к этому заданию:
Задание 1161
Решите неравенство: $$\frac{-16}{(x+2)^2 - 5} \le 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Числитель $$-16$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была отрицательной, знаменатель должен быть положительным: $$(x+2)^2 - 5 > 0.$$
2) Решим неравенство: $$(x+2)^2 - 5 > 0.$$ Учтем, что $$(x+2)^2 - 5 = (x + 2)^2 - (\sqrt{5})^2 = (x+2-\sqrt{5})(x+2+\sqrt{5}).$$ Нули $$x_1 = -2 - \sqrt{5}; x_2 = -2 + \sqrt{5}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x+2-\sqrt{5})(x+2+\sqrt{5})$$ на полученных промежутках:
Выражение положительное при: $$x \in (-\infty;\,-2-\sqrt{5}) \;\cup\; (-2+\sqrt{5};\,+\infty).$$
Задание 1172
Решите неравенство: $$\frac{-18}{(x+4)^2 - 10} \ge 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Числитель $$-18$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была положительной, знаменатель должен быть отрицательным: $$(x+4)^2 - 10 < 0.$$
2) Решим неравенство: $$(x+4)^2 - 10 < 0.$$ Учтём, что $$(x+4)^2 - 10 = (x + 4)^2 - (\sqrt{10})^2 = (x+4-\sqrt{10})(x+4+\sqrt{10}).$$ Нули $$x_1 = -4 - \sqrt{10};\quad x_2 = -4 + \sqrt{10}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x+4-\sqrt{10})(x+4+\sqrt{10})$$ на полученных промежутках:
Выражение отрицательное при: $$x \in (-4-\sqrt{10};\,-4+\sqrt{10}).$$