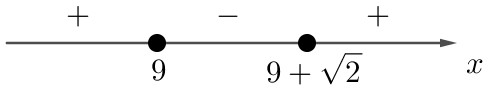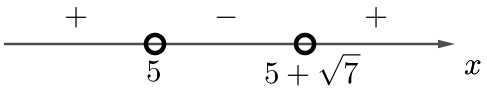Задание 4651
Задание 4651
Решите неравенство: $$(x - 7)^{2} < \sqrt{11}(x - 7)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$(x-7)^{2}-\sqrt{11}(x-7)<0$$
$$(x-7)(x-7-\sqrt{11})<0$$
Начертим координатную прямую, отметим значения х при которых выражение $$(x-7)(x-7-\sqrt{11})$$ равно нулю и расставим знаки значений, которые принимает данное выражение на полученных промежутках:
Выберем те, в которых выражение принимает отрицательные значения: $$(7; 7+\sqrt{11})$$
Аналоги к этому заданию:
Задание 2189
Решите неравенство: $$(x - 9)^2 \ge \sqrt{2}(x - 9)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Переносим всё в левую часть: $$(x - 9)^2 - \sqrt{2}(x - 9) \ge 0.$$ Выносим общий множитель: $$(x - 9)\bigl((x - 9) - \sqrt{2}\bigr) \ge 0.$$ То есть $$(x - 9)(x - 9 - \sqrt{2}) \ge 0.$$
2) Нули: $$x_1 = 9; x_2 = 9 + \sqrt{2}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 9)(x - 9 - \sqrt{2})$$ на полученных интервалах:
Выражение неотрицательно при: $$x \in (-\infty;\, 9] \cup [9 + \sqrt{2};\, +\infty).$$
Задание 1054
Решите неравенство: $$(x - 3)^2 \sqrt{5}(x - 3)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Перенесём всё в левую часть: $$(x - 3)^2 - \sqrt{5}(x - 3) < 0.$$ Вынесём общий множитель: $$(x - 3)\bigl((x - 3) - \sqrt{5}\bigr) < 0.$$ То есть $$(x - 3)(x - 3 - \sqrt{5}) < 0.$$
2) Нули выражения: $$x_1 = 3, x_2 = 3 + \sqrt{5}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 3)(x - 3 - \sqrt{5})$$ на полученных интервалах:
Выражение отрицательно при: $$x \in (3;\, 3 + \sqrt{5}).$$
Задание 1069
Решите неравенство: $$(x - 5)^2 \sqrt{7}(x - 5)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Переносим всё в левую часть: $$(x - 5)^2 - \sqrt{7}(x - 5) < 0.$$ Выносим общий множитель: $$(x - 5)\bigl((x - 5) - \sqrt{7}\bigr) < 0.$$ То есть $$(x - 5)(x - 5 - \sqrt{7}) < 0.$$
2) Нули: $$x_1 = 5, x_2 = 5 + \sqrt{7}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 5)(x - 5 - \sqrt{7})$$ на полученных интервалах:
Выражение отрицателено при: $$x \in (5;\, 5 + \sqrt{7}).$$