Уравнения, неравенства и их системы
Задание 3893
На каком из рисунков изображено множество решений неравенства $$7x - x^2 0$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3057
На каком рисунке изображено множество решений неравенства $$4x + 5 \ge 6x - 2$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$4x+5\geq 6x-2\Leftrightarrow$$ $$4x-6x\geq -2-5\Leftrightarrow$$ $$-2x\geq -7\Leftrightarrow$$ $$x\leq 3,5$$, что соответствует 2 варианту ответа.
Задание 2986
На каком рисунке изображено множество решений неравенства $$9 - 3(x + 2) > 4 - x$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$9-3(x+2)>4-x\Leftrightarrow$$ $$9-3x-6-4+x>0\Leftrightarrow$$ $$-2x-1>0\Leftrightarrow$$ $$-2x>1\Leftrightarrow$$ $$x<-\frac{1}{2}$$, что соответствует 2 варианту ответа.
Задание 3486
На каком рисунке изображено множество решений неравенства $$x^2 - 2x - 3 \ge 0$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Решим уравнение $$x^{2}-2x-3=0$$
$$\left\{\begin{matrix}x_{1} +x_{2}=2& & \\x_{1}*x_{2}=-3 & &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x_{1}=3 & & \\x_{2}=-1 & &\end{matrix}\right.$$
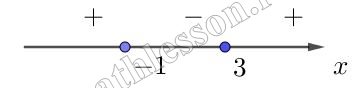
Отметим полученные точки на координатной прямой и расставим знаки выражения
Нам нужны неотрицательные значения $$\Rightarrow x\in (-\infty ;-1] \cup [3 ;+\infty ]$$, соответствует 2 варианту ответа.
Задание 4928
На каком рисунке изображено множество решений неравенства $$x^2 - 4x + 3 \ge 0$$?
1) $$( -\infty;\ 1 ] \cup [ 3;\ +\infty )$$
2) $$( -\infty;\ 1 ) \cup ( 3;\ +\infty )$$
3) $$[ 1;\ 3 ]$$
4) $$( 1;\ 3 )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Приравняем выражение слева к нулю: $$x^{2}-4x+3\geq 0 \Leftrightarrow$$$$x=1;3$$
Отметим полученные точки на координатной прямой (закрашенные, так как неравенство нестрогое).
Расставим знаки, которые принимает выражение на полученных промежутках (путем подстановки значений с этих промежутков в данное выражение):
Выберем те, где получен знак $$+$$. Тогда $$x \in (-\infty ;1]\cup [3;+\infty)$$, что соответствует 3 варианту ответа
Задание 3151
На каком рисунке изображено множество решений системы неравенств: $$\left\{\begin{aligned} 2x - 3 < 1 \\ 5 - 3x > 8 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$\left\{\begin{matrix}2x-3<1\\5-3x>8\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2x<4\\-3x>3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x<2\\x<-1\end{matrix}\right.\Leftrightarrow$$ $$x<-1$$, что соответствует 3 варианту ответа ( т.к. $$(-4;1) \in (-\infty ;-1)$$ )
Задание 3125
На каком рисунке изображено множество решений системы неравенств:
$$\left\{\begin{aligned}-12 + 3x > 0\\9 - 4x > -3\end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$\left\{\begin{matrix} -12+3x>0\\ 9-4x>-3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} 3x>12\\ 9+3x>4x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} x>4\\ x<3\end{matrix}\right.\Leftrightarrow$$ $$x \in \varnothing$$, что соответсвует 4 варианту .
Задание 2938
На каком рисунке изображено множество решений системы неравенств:
$$\left\{\begin{aligned}2(x+2) - 7 & 15\\-3x + 12 & 0\end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$\left\{\begin{matrix}2(x+2)-7<15\\-3x+12<0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}2x+4-7-15<0\\3x-12>0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}2x<8\\3x>12\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x<9\\x>4\end{matrix}\right.$$
Получим $$x \in (4;9)$$ , что соответствует 1 варианту ответа.
Задание 4917
Найдите наибольшее значение $$x$$, удовлетворяющее системе неравенств:
$$\left\{\begin{aligned} 2x + 12 \ge 0 \\ x + 5 \le 2 \end{aligned}\right.$$
$$\left\{\begin{matrix}2x+12\geq0\\x+5\leq2\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}2x\geq-12|:2\\x\leq2-5\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x\geq-6|:2\\x\leq-3\end{matrix}\right.\Leftrightarrow$$$$x \in [-6;-3]$$. Наибольшее значение в таком случае составляет -3
Задание 1943
Найдите решение системы неравенств:
$$\left\{\begin{aligned}x + 0,6 &\le 0\\x - 1 &\ge -4\end{aligned}\right.$$
1) $$( -\infty;\ -3 ]$$
2) $$[ -0,6;\ +\infty )$$
3) $$( -\infty;\ -3 ];\ [ -0,6;\ +\infty )$$
4) $$[ -3;\ -0,6 ]$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3297
При каких значениях $$a$$ выражение $$12 - 0,3a$$ принимает положительные значения?
1) $$a > 40$$
2) $$a 40$$
3) $$a -40$$
4) $$a > -40$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$12-0,3a>0\Leftrightarrow$$ $$-0,3a>-12\Leftrightarrow$$$$a<40$$, что соответствует 2 варианту ответа
Задание 4920
При каких значениях $$a$$ выражение $$5a + 9$$ принимает отрицательные значения?
1) $$a > -\frac{9}{5}$$
2) $$a -\frac{5}{9}$$
3) $$a > -\frac{5}{9}$$
4) $$a -\frac{9}{5}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$5a+9<0 \Leftrightarrow$$$$5a<-9|:5\Leftrightarrow$$$$a<-\frac{9}{5}$$, что соответствует 4 варианту ответа.
Задание 1305
При каких значениях $$a$$ выражение $$9a + 4$$ принимает положительные значения? В ответе укажите номер правильного варианта ответа.
1. $$a > -\frac{9}{4}$$
2. $$a -\frac{4}{9}$$
3. $$a -\frac{9}{4}$$
4. $$a >-\frac{4}{9}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3275
При каких значениях $$x$$ значение выражения $$6x - 2$$ меньше значения выражения $$7x + 8$$?
1) $$x > -10$$
2) $$x -10$$
3) $$x -6$$
4) $$x > -6$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$6x-2<7x+8\Leftrightarrow$$ $$-2-8<7x-6x\Leftrightarrow$$ $$x>-10$$, что соответствует 1 варианту ответа
Задание 4921
Решение какого из данных неравенств изображено на рисунке?
1) $$x^2 - 6x 0$$
2) $$x^2 - 6x > 0$$
3) $$x^2 - 36x 0$$
4) $$x^2 - 36x > 0$$
