Фигуры на квадратной решётке
Задание 2705
В треугольнике $$ABC$$ $$AB = BC = 3\sqrt{5}$$, высота $$CH$$ равна $$3$$. Найдите $$tg A$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 662
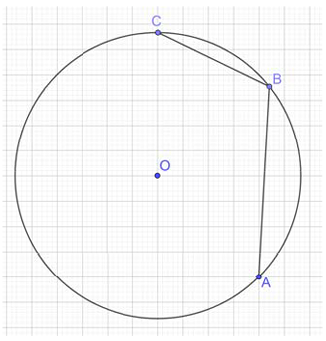
Согласно рисунку градусная мера центрального угла АОС равна $$45°+90° = 135°$$. Следовательно, дуга, на которую опирается вписанный в окружность угол АВС имеет градусную меру:
$$360°-135° = 225°$$.
По теореме о величине угла, вписанного в окружность, получаем, что градусная мера угла АВС:
$$\frac{225°}{2} = 112,5°$$.
Задание 986
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1424
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1444
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1023
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 129
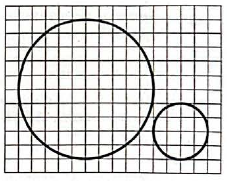
Отношение площадей кругов равно квадрату отношения радиусов. $$R_1 = 5; R_2 = 2$$ клеток.
Радиусы относятся как $$5:2$$, то площади как $$25:4 = 6,25$$
Задание 2386
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1796
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3007
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


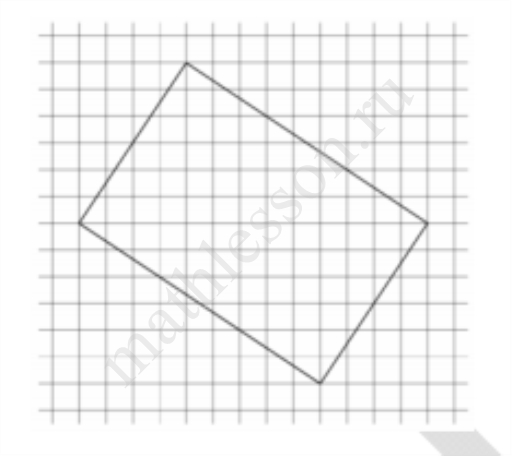
Сторона a=6; высота: h=6. Тогда площадь: S=ah=6*6=36
Задание 1391
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1750
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!