Комбинация многоугольников и окружностей
Задание 1913
Биссектриса $$CM$$ треугольника $$ABC$$ делит сторону $$AB$$ на отрезки $$AM=4$$ и $$MB=9$$. Касательная к окружности, описанной около треугольника $$ABC$$, проходит через точку $$C$$ и пересекает прямую $$AB$$ в точке $$D$$. Найдите $$CD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1854
В прямоугольном треугольнике $$ABC$$ катет $$AC$$ равен $$8$$, а катет $$BC=15$$. Найдите диаметр окружности, которая проходит через концы гипотенузы и касается прямой $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4133
В прямоугольном треугольнике $$ABC$$ с гипотенузой $$AB$$, равной 10, на высоте $$CD$$ как на диаметре построена окружность. Касательные к этой окружности, проходящие через точки $$A$$ и $$B$$, пересекаются при продолжении в точке $$K$$. Чему равны касательные к окружности, выходящие из точки $$K$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$HB=x\Rightarrow AH=10-x$$
по свойству касательных $$MB=HB=x$$
$$AH=AN=10-x$$; пусть $$OH=OC=r$$;
$$KN=KM=z$$
2) По свойству высоты прямоугольного треугольинка:
$$CH=\sqrt{AH\cdot HB}\Leftrightarrow(2r)^{2}=x(10-x)$$
$$\Leftrightarrow r^{2}=\frac{x(10-x)}{4}$$
3) $$S_{AKB}=p\cdot r$$, где
$$p=\frac{AK+KB+AB}{2}$$
$$S=\sqrt{p(p-AK)(P-KB)(p-AB)}$$
$$p=\frac{10+10-x+x+2z}{2}=10+z$$
$$S=\sqrt{(10+z)(10+z-10+x-x)(10+z-x-z)(10+z-10}=$$
$$=\sqrt{(10+z)\cdot x\cdot(10-x)\cdot z}$$
Тогда:
$$r=\frac{S}{p}=\frac{xz(10+z)(10-x)}{10+z}=\sqrt{\frac{xz(10-x)}{10+z}}$$
4) 2 из 3:
$$\sqrt{\frac{x(10-x)}{4}}=\sqrt{\frac{xz(10-x)}{10+z}}$$
$$\frac{1}{4}=\frac{z}{10+z}$$
$$10+z=4z\Leftrightarrow z=\frac{10}{3}$$
Задание 3216
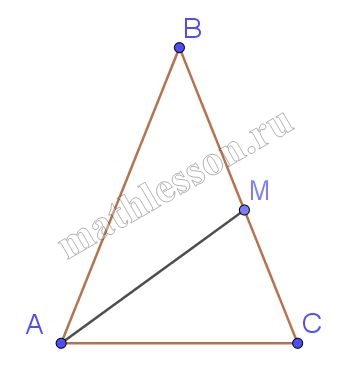
В равнобедренном треугольнике $$ABC$$ ($$AB=BC$$) проведена биссектриса $$AM$$. Известно, что $$BC:MC=5:2$$. Найдите отношение длины отрезка $$MC$$ к радиусу окружности, описанной около треугольника $$AMC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) $$BC:MC =5:2\Rightarrow$$ $$BM:MC=3:2$$. Пусть $$BM=3y\Rightarrow$$ $$MC=2y, BC=5y$$
2) По свойству биссектрисы: $$\frac{AB}{AC}=\frac{BM}{MC}\Rightarrow$$ $$\frac{AB}{AC}=\frac{3}{2}$$. $$AB=BC=5y\Rightarrow$$ $$AC=\frac{5*2y}{3}=\frac{10y}{3}$$
3) $$AM=\sqrt{AB*AC-BM*MC}=$$$$\sqrt{5y*\frac{10y}{3}-3y*2y}=$$$$\sqrt{\frac{50y^{2}-12y^{2}}{3}}=$$$$\sqrt{\frac{32 y^{2}}{3}}=$$$$4y\sqrt{\frac{2}{3}}$$
4) $$S_{AMC}=S_{ABC}*\frac{MC}{BC}$$, $$p_{ABC}=5y+5y+\frac{10y}{3}=\frac{20y}{3}$$
$$S_{ABC}=\sqrt{\frac{20y}{3}*(\frac{20y}{3}-5y)^{2}(\frac{20y}{3}-\frac{10y}{3})}=$$$$\frac{50y^{2}\sqrt{2}}{9}\Rightarrow$$
$$S_{AMC}=\frac{2}{5}*\frac{50y^{2}\sqrt{2}}{9}=$$$$\frac{20y^{2}\sqrt{2}}{9}$$
5) $$R=\frac{MC*AC}{4 S_{AMC}}\Rightarrow$$ $$\frac{MC}{R}=\frac{4 S_{AMC}}{AM*AC}=$$$$\frac{4*20y^{2}\sqrt{2}}{9}:(4y\frac{\sqrt{2}}{\sqrt{3}}*\frac{10y}{3})=$$$$\frac{2\sqrt{3}}{3}$$
Задание 4028
В равностороннем треугольнике $$ABC$$ из вершин $$A$$ и $$B$$ проведена окружность с центром в точке $$O$$, проходящая через точку пересечения медиан треугольника $$ABC$$ и касающаяся его стороны $$BC$$ в её середине $$D$$. Из точки $$A$$ проведена прямая, касающаяся этой окружности в точке $$E$$ так, что градусная мера угла $$BAE$$ меньше $$30^{\circ}$$. Найдите отношение площадей треугольника $$ABE$$ и четырехугольника $$BEOD$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4258
В равностороннем треугольнике $$ABC$$ точка $$M$$ делит основание $$AC$$ на отрезки $$5$$ и $$3$$. В треугольники $$ABM$$ и $$CBM$$ вписаны окружности. Найдите площадь фигуры, вершинами которой являются центры окружностей и точки их касания со стороной $$BM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2635
В трапецию, у которой меньшее основание равно $$5$$, вписана окружность. Одна из боковых сторон трапеции делится точкой касания на отрезки $$9$$ и $$4$$, считая от большего основания. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2336
В треугольнике $$ABC$$ известны длины сторон $$AB=28$$, $$AC=56$$, точка $$O$$ - центр окружности, описанной около треугольника $$ABC$$. Прямая $$BD$$, перпендикулярная прямой $$AO$$, пересекает сторону $$AC$$ в точке $$D$$. Найдите $$CD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3954
В треугольнике $$ABC$$ угол $$B$$ равен $$30^{\circ}$$. Через точки $$A$$ и $$B$$ проведена окружность радиуса $$2$$, касающаяся прямой $$AC$$ в точке $$A$$. Через точки $$B$$ и $$C$$ проведена окружность радиуса $$3$$, касающаяся прямой $$AC$$ в точке $$C$$. Найдите длину стороны $$AC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) $$O_{1}$$ - ценрт оружности $$R_{1}=2$$; $$O_{2}$$ - ценрт оружности $$R_{2}=3$$; $$\angle ABC=\alpha$$; $$\angle BAC=\beta$$;
2) $$\angle BO_{2}C=2\angle BCA=2\alpha$$; $$\angle AO_{1}B=2\angle BAC=2\beta$$;
3) $$AB=2R_{1}\sin\beta=4\sin\beta$$; $$BC=2R_{2}\sin\alpha=6\sin\alpha$$; (по теореме синусов) $$\frac{AB}{\sin\alpha}=\frac{BC}{\sin\beta}$$ (из $$\bigtriangleup ABC$$) $$\Rightarrow$$ $$\frac{4\sin\beta}{\sin\alpha}=\frac{6\sin\alpha}{\sin\beta}$$ $$\Leftrightarrow$$ $$4\sin^{2}\beta=6\sin^{2}\alpha$$ $$\Leftrightarrow$$ $$\frac{\sin\beta}{\sin\alpha}=\sqrt{\frac{3}{2}}$$
4) $$\frac{AC}{\sin\angle ABC}=\frac{AB}{\sin\angle ACB}$$ $$\Rightarrow$$ $$AC=\frac{AB}{\sin\angle ACB}\cdot\sin\angle ABC=$$ $$\frac{4\sin\beta}{\sin\alpha}\cdot\sin30^{\circ}=4\cdot\frac{\sqrt{3}}{\sqrt{2}}\cdot\frac{1}{2}=\sqrt{6}$$
Задание 4051
В треугольнике, величина одного из углов которого равна разности величин двух других его углов, длина меньшей стороны равна $$1$$, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найдите длину большей стороны треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Построим рисунок:
1) Пусть меньший угол $$\alpha$$, а жва других $$x$$ и $$y$$. По условию задания меньший равен равности двух сотавшихся, а по свойству треугольника разность 180 и меньшего дает сумму оставшихся. Тогда:
$$\left\{\begin{matrix} \alpha= x-y\\180-\alpha =x+y \end{matrix}\right.$$
Сложим оба уравнения системы:
$$\Rightarrow 180=2x \Leftrightarrow x=90$$
То есть мы получили прямоугольный треугольник. Построим новый чертеж по условию задачи и с учетом полученного решения:
2) Пусть $$AC = x ; S_{AEDC}=S_{1}; S_{BCIH}=S_{2}$$. Тогда $$S_{1}=x^{2} ;$$$$ BC=\sqrt{x^{2}-1} \Rightarrow S_{2}=x^{2}-1 \Rightarrow $$$$S_{1}+S_{2}=2x^{2}-1$$
3)Пусть площадь окружности $$S_{3} ; R$$-радиус окружности.Радиус описанной окружотсти вокруг прямоугольного треугольника равен полвине его гипотенузы. $$R=\frac{AC}{2}=\frac{x}{2}$$. Тогда : $$S_{3}=\pi R^{2}=\pi \frac{x^{2}}{4}$$. Приравняем площади: $$2x^{2}-1=2*\pi \frac{x^{2}}{4} \Rightarrow $$$$4x^{2}-2=\pi x^{2} \Rightarrow $$$$x^{2}(4-\pi)=2 \Rightarrow $$$$x=\sqrt{\frac{2}{4-\pi}}$$