(C3) Функции и их свойства. Графики функций
Задание 3451
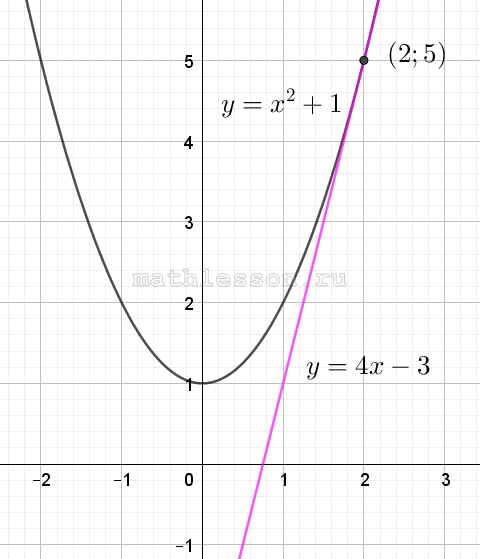
Известно, что графики функций $$y = x^2 + p$$ и $$y = 4x - 3$$ имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- Так как графики имеют одну точку пересечения, то уравнение : $$x^{2}-p=4x-3$$ должно иметь один корень, то есть дискриминант равен 0:
- $$x^{2}-4x+p+3=0$$ $$D=16-4(p+3)=16-4p+12=4-4p=0$$
- Тогда $$p=1$$.
- Найдем абсциссу точки пересечения: $$x_{0}=-\frac{-4}{2}=2$$.
- Найдем ординату (подставим в линейное уравнение): $$y=4*2-3=5$$. То есть точка пересечения будет с координатами (2;5).
- Построим графики функций:
Задание 4276
Найдите все значения $$a$$, при каждом из которых уравнение $$|3x + 2| + |3x - 2| = ax + 4$$ имеет ровно два решения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3428
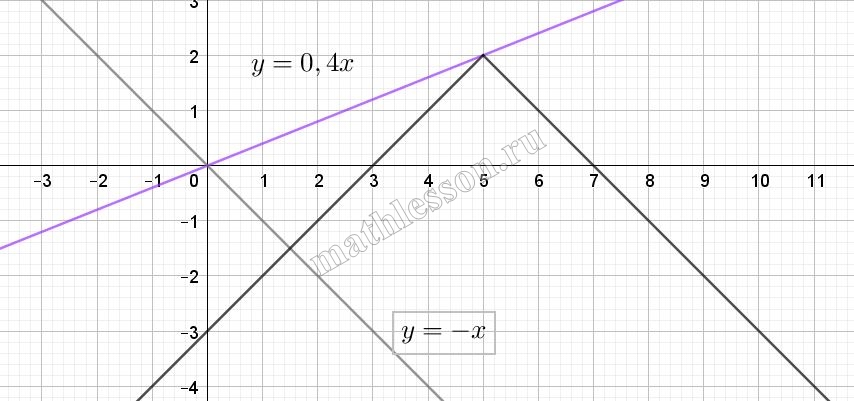
Найдите все значения $$k$$, при которых прямая $$y = kx$$ пересекает в двух точках ломаную, заданную условиями: $$y = \left\{\begin{aligned} x - 3,& x < 5 \\ 7 - x,& x \ge 5 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$y=\left\{\begin{matrix}x-3, x<5 & & \\7-x, x\geq 5& &\end{matrix}\right.$$
Начертим график данной функции :
При a>0 до момента , когда пройдет поезд (5;2) (прямая розового цвета) : $$2=5*k\Rightarrow k=0,4$$, то есть $$k\in [0; 0,4)$$.
При a<0, пока не станет параллельна (прямая серого цвета) прямой y=7-x, то есть $$a\in (-1; 0)$$ Итог (-1; 0,4)
Задание 1213
Найдите наибольшее значение выражения $$\frac{x^3 - y}{x^2 + 1} - \frac{x^2y - x}{x^2 + 1}$$, если $$x$$ и $$y$$ связаны соотношением $$y = x^2 + x - 4$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 848
Первая прямая проходит через точки $$\left(0;\,\frac{9}{2}\right)$$ и $$(3;\,6)$$. Вторая прямая проходит через точки $$(1;\,2)$$ и $$(-4;\,7)$$. Найдите координаты общей точки этих двух прямых.
Уравнение первой прямой
$$\frac{x}{3}=\frac{y-4,5}{1,5}$$
$$1,5x-3y+13,5=0 $$
Уравнение второй прямой
$$\frac{x-1}{-5}=\frac{y-2}{5}$$
$$5x+5y-15=0$$
$$\left\{\begin{matrix} 3y-1,5x=13,5\\ x+y=3 \end{matrix}\right.$$
$$x=3-y$$
$$3y-1,5(3-y)=13,5$$
$$3y-4,5+1,5y=13,5$$
$$4,5y=18$$
$$y=4$$
$$x=-1$$
$$(-1;4)$$
Задание 3816
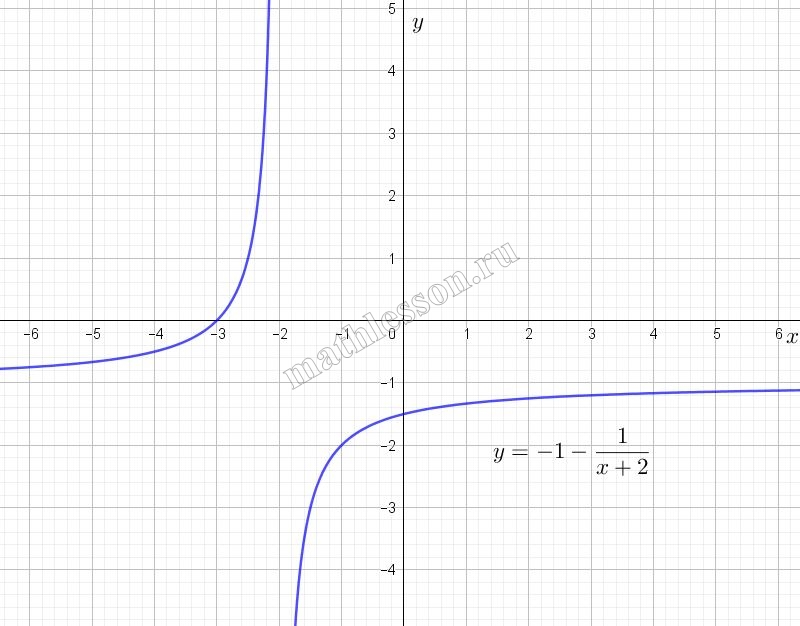
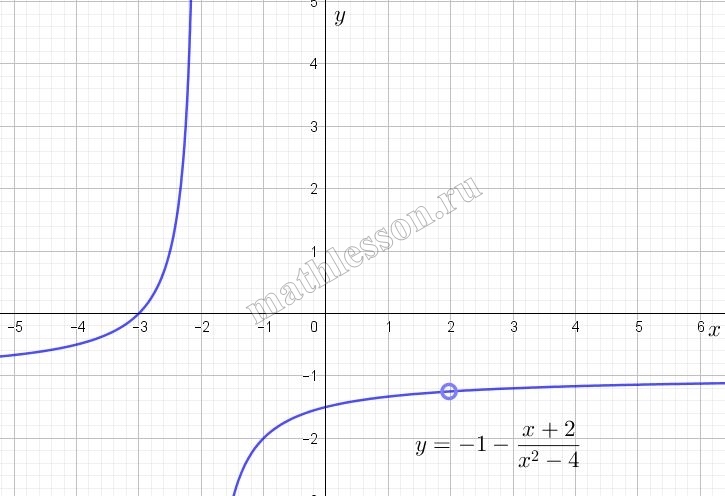
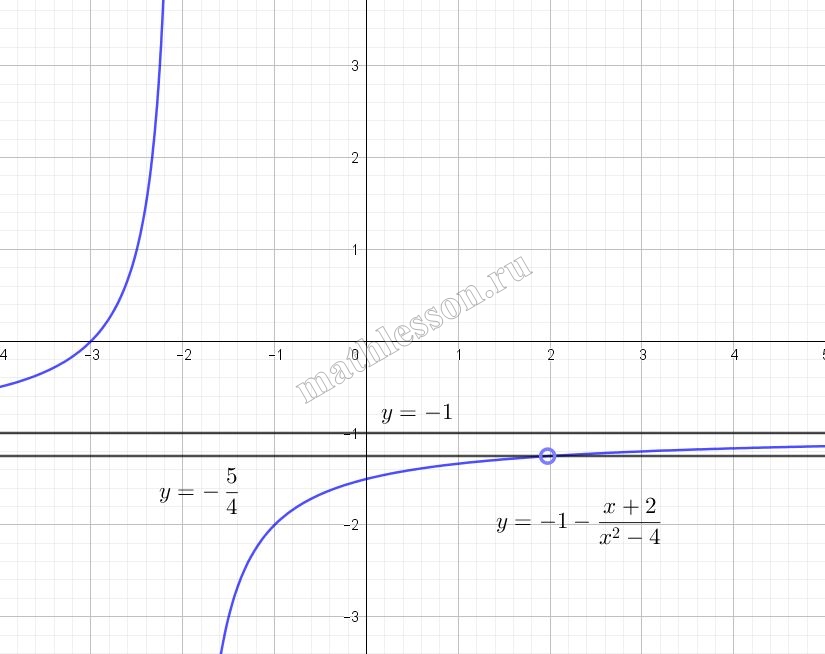
Постройте график функции $$y = -1 - \frac{x - 2}{x^2 - 4}$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


ОДЗ: $$x^{2}-4 \neq 0 \Leftrightarrow$$$$x\neq\pm 2$$. Преобразуем правую часть функции: $$-1-\frac{x-2}{x^{2}-4}=$$$$-1-\frac{x-2}{(x-2)(x+2)}=$$$$-1-\frac{1}{x+2}$$
То есть график функции $$y_{1}=-1-\frac{1}{x+2}$$ и график искомой функции совпадают, если к $$y_{1}$$ применить ОДЗ для искомой. График функции $$y_{1}$$ - гипербола, смещенная на 1 единицу вних и на две влево относительно графика эталонной обратной пропорциональности $$y=\frac{1}{x}$$. Начертим график функции $$y_{1}$$:
Учтем, что $$x\neq\pm 2$$. В случае $$x\neq -2$$ можно отдельно не рассматривать, так как это условие уже выполняется для графика функции $$y_{1}$$. Для $$x\neq 2$$: подставим значение $$x=2$$ в функции $$y_{1}$$: $$y_{1}(2)=-1-\frac{1}{2+2}=-\frac{5}{4}$$. То есть точку, с координатами $$(2;-\frac{5}{4})$$ необходимо отметить пустой на графике функции $$y_{1}$$ и тогда мы получим график искомой функции:
Прямая $$y=a$$ - прямая паралленая оси Ох, чтобы она не имела с графиком искомой функции точек пересечения она должны использоваться следующие значения $$a=-1;-\frac{5}{4}$$:
Задание 1192
Постройте график функции $$y = -4 - \frac{x^4 + x^3}{x^2 + x}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3934
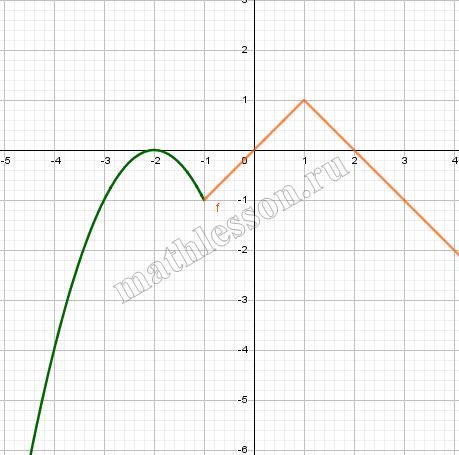
Постройте график функции $$y = \begin{cases} -x^2 - 4x - 4,& x -1 \\ 1 - |x - 1|,& x \ge -1 \end{cases}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4031
Постройте график функции $$y = \frac{(\sqrt{x^2 - 5x + 6})^2}{x - 3}$$ и найдите все значения $$a$$, при которых прямая $$y = a$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1552
Постройте график функции $$y = \frac{(0{,}25x^2 + 0{,}5x) \cdot |x|}{x + 2}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3795
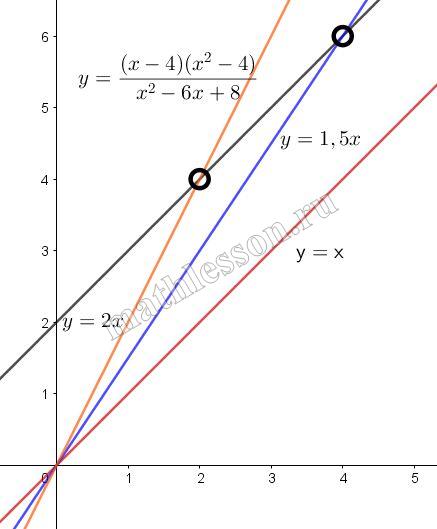
Постройте график функции $$y = \frac{(x - 4)(x^2 - 4)}{x^2 - 6x + 8}$$ и определите, при каких значениях $$k$$ построенный график не будет иметь общих точек с прямой $$y = kx$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Найдем область определения заданной функции: $$x^{2}-6x+8 \neq 0 \Leftrightarrow $$$$x_{1} \neq 2 ; 4$$
Преобразуем данную функцию с учетом полученной области определения: $$\frac{(x-4)(x^{2}-4)}{x^{2}-6x+8}=$$$$\frac{(x-4)(x-2)(x+2)}{(x-4)(x-2)}=x+2$$. То есть график функции $$y=x+2$$ совпадает с графиком начальной функции при наличии области ее определения.
Получаем, что точки (2;4) и (4;6) пустые, следовательно, чтобы прямая y=kx не имела с графиком пересечений, она должна пройти через эти точки. Подставим их координаты в уравнение прямой, чтобы найти k:
$$4=2k \Leftrightarrow$$$$k=2$$
$$6=4k \Leftrightarrow$$$$k=1,5$$
Так же прямая не будет иметь пересечений, если она будет параллельна графику начальной функции. Две прямые $$y_{1}=k_{1}x+b_{1}$$ и $$y_{2}=k_{2}x+b_{2}$$ параллельны в том случае, если коэффициенты при х у них одинаковы ($$k_{1}=k_{2}$$, а свободные - разные ($$b_{1} \neq b_{2}$$). То есть k=1 тоже будет ответом.