ОГЭ 2026. Вариант 3 Ященко 36 вариантов ФИПИ школе.
Решаем 3 вариант ОГЭ Ященко 2026 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 3 варианта (всех заданий) Ященко 2026 ФИПИ 36 вариантов.
Рутуб
Ютуб
Задания:
Задание 1-5
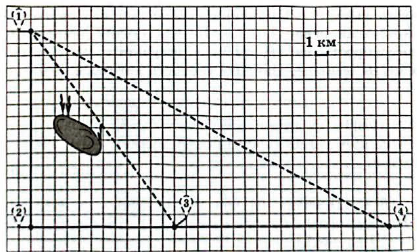
Миша летом отдыхает с папой в деревне Починки. В среду они собираются съездить на велосипедах в село Игнатово. Из деревни Починки в село Игнатово можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Власово до деревни Крынки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Игнатово. Есть и третий маршрут: в деревне Власово можно свернуть на прямую грунтовую дорогу в село Игнатово, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Миша с папой едут со скоростью $$20$$ км/ч, а по грунтовой дороге — со скоростью $$15$$ км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна $$1$$ км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Насел. пункты | д. Крынки | с. Игнатово | д. Починки |
| Цифры |
2. Найдите расстояние от деревни Починки до села Игнатово по прямой. Ответ дайте в километрах.
3. Сколько минут затратят на дорогу из деревни Починки в село Игнатово Миша с папой, если поедут через деревню Крынки?
4. На сколько процентов расстояние от села Игнатово до деревни Власово через деревню Крынки больше расстояния между этими пунктами по прямой?
5. В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в селе Игнатово и в деревнях Починки, Власово и Крынки.
| Наименование продукта | д. Починки | с. Игнатово | д. Крынки | д. Власово |
| Молоко (1 л) | 85 | 80 | 90 | 105 |
| Хлеб (1 батон) | 65 | 55 | 60 | 45 |
| Сыр «Сливочный» (1 кг) | 600 | 550 | 500 | 580 |
| Говядина (1 кг) | 730 | 750 | 700 | 790 |
| Картофель (1 кг) | 85 | 80 | 90 | 75 |
Миша с папой хотят купить $$2$$ л молока, $$2$$ кг говядины и $$4$$ кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
1) по прямолинейному шоссе через деревню Власово до деревни Крынки, где нужно повернуть под прямым углом налево (в задании опечатка, на самом деле поворот направо - следовательно, $$3$$ - Власово, $$2$$ - Крынки, $$4$$ - Починки, $$1$$ - Игнатьево
Тогда ответ: $$214$$
2) С учетом, что $$1$$ клетка по масштабу равна $$1$$ км, то расстояние (по первым буквам названия населенного пункта): ПВ: 18 км; ВК: 12 км; КИ: 16 км. Тогда: ПВК: 30 км.
ПИ: $$\sqrt{30^2 + 16^2} = \sqrt{1156} = 34$$ км.
3) Общее расстояние по шоссе $$18 + 12 + 16 = 46$$ км. Скорость движения по шоссе $$20$$ км/ч. Тогда время в минутах: $$\frac{46}{20}\cdot 60 = 138$$ минут.
4) ВИ: $$\sqrt{12^2 + 16^2} = 20$$ км. ВКИ: $$12 + 16 = 28$$ км. Разность расстояний $$8$$ км. Составим пропорцию:
20 км - 100%
8 км - х %
$$x = \frac{8 \cdot 100}{20} = 40\%$$
5) Распишем стоимость продуктового набора для каждого населенного пункта:
П: $$2 \cdot 85 + 2 \cdot 730 + 4 \cdot 85 = 1970$$
И: $$2 \cdot 80 + 2 \cdot 750 + 4 \cdot 80 = 1980$$
К: $$2 \cdot 90 + 2 \cdot 700 + 4 \cdot 90 = 1940$$ - наименьшая стоимость.
В: $$2 \cdot 105 + 2 \cdot 790 + 4 \cdot 75 = 2090$$
Задание 7
Какое из чисел $$\frac{65}{18}$$, $$\frac{71}{18}$$, $$\frac{79}{18}$$ и $$\frac{95}{18}$$ принадлежит отрезку $$[4 ; 5]$$:
1) $$\frac{65}{18}$$
2) $$\frac{71}{18}$$
3) $$\frac{79}{18}$$
4) $$\frac{95}{18}$$
В ответе запишите номер выбранного числа.
$$\frac{65}{18} \approx 3,61$$, $$\frac{71}{18} \approx 3,94$$, $$\frac{79}{18} \approx 4,39$$, $$\frac{95}{18} \approx 5,28$$
По условию должно принадлежать отрезку $$[4; 5]$$
Подходит $$\frac{79}{18}$$ → номер $$3$$
Задание 8
Найдите значение выражения $$\frac{b^{13} \cdot (c^8)^2}{(b \cdot c)^{15}}$$ при $$c = 6$$ и $$b = \sqrt{5}$$.
$$\frac{b^{13} \cdot (c^8)^2}{(b \cdot c)^{15}} = \frac{b^{13} \cdot c^{16}}{b^{15} \cdot c^{15}} = b^{-2} \cdot c^{1} = (\sqrt{5})^(-2) \cdot 6$$$$= \frac{1}{(\sqrt{5})^(2)} \cdot 6 = \frac{1}{5} \ cdot 6 = \frac{6}{5} = 1,2$$
Задание 10
В некотором случайном опыте случайное событие $$B$$ имеет вероятность $$0,68$$. Найдите вероятность противоположного события.
Сумма вероятностей противоположных событий равна $$1$$. Тогда:
$$P(\bar{B}) = 1 - P(B) = 1 - 0,68 = 0,32$$
Задание 11
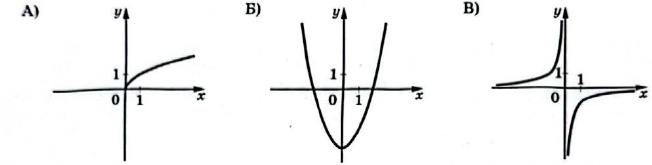
А) ветвь параболы в первой четверти → $$1$$
Б) парабола с вершиной в $$(0; y)$$ → $$3$$
Б) гипербола во $$2$$-й и $$4$$-й четвертях → $$2$$
Задание 12
Теорему синусов можно записать в виде $$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}$$, где $$a$$ и $$b$$ — две стороны треугольника, а $$\alpha$$ и $$\beta$$ — углы треугольника, лежащие против них соответственно. Пользуясь этой формулой, найдите $$a$$, если $$b = 24$$, $$\sin \alpha = 0,3$$ и $$\sin \beta = 0,5$$.
Подставим известные значения в формулу:
$$\frac{a}{0,3} = \frac{24}{0,5}$$
$$\frac{a}{0,3} = 48$$
$$a = 48 \cdot 0,3 = 14,4$$
Задание 14
Каучуковый мячик с силой бросили на асфальт. Отскочив, мячик подпрыгнул на $$3,6$$ м, а при каждом следующем прыжке он поднимался на высоту в два раза меньше предыдущей. При каком по счёту прыжке мячик первый раз не достигнет высоты $$15$$ см?
$$3,6$$ м = $$360$$ см
Высоты: $$360$$, $$180$$, $$90$$, $$45$$, $$22,5$$ см
На $$5$$-м прыжке высота $$22,5 15$$? Нет, $$22,5 > 15$$
$$6$$-й прыжок: $$11,25 15$$ см
Задание 16
В треугольнике $$ABC$$ известно, что $$AC = 12$$, $$BC = 35$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус описанной около этого треугольника окружности.
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы
Гипотенуза $$AB = \sqrt{AC^2 + BC^2} = \sqrt{144 + 1225} = \sqrt{1369} = 37$$
$$R = \frac{37}{2} = 18,5$$
Задание 17
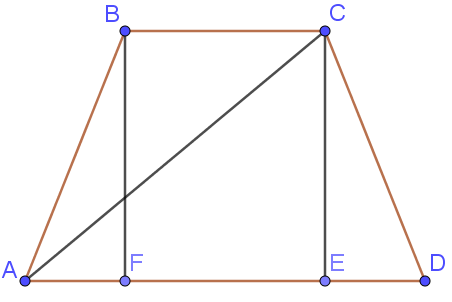
Диагональ равнобедренной трапеции образует с её основанием угол $$45^\circ$$. Найдите длину высоты трапеции, если её основания равны $$3$$ и $$4$$.
Пусть $$BF$$ и $$CE$$ - высоты. Тогда $$BCEF$$ - прямоугольник и $$BC = FE = 3$$
Треугольники $$ABF$$ и $$CED$$ - равны по катету и гипотенузе, тогда $$AF = \frac{AD-BC}{2} = 0,5$$
$$\angle CAE = 45^\circ$$, то есть треугольник $$AEC$$ - прямоугольный и равнобедренный, тогда $$CE = AE = 0,5 + 3 = 3,5$$
Задание 18
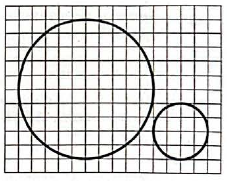
Отношение площадей кругов равно квадрату отношения радиусов. $$R_1 = 5; R_2 = 2$$ клеток.
Радиусы относятся как $$5:2$$, то площади как $$25:4 = 6,25$$
Задание 19
Какие из следующих утверждений являются истинными высказываниями?
- В любом ромбе все углы равны.
- Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
- Неверно - в ромбе противоположные углы равны, но не обязательно все
- Верно - аксиома параллельных прямых
- Верно - признак подобия по двум углам
Задание 20
Решите неравенство $$-\frac{14}{x^2 + 5x - 14} \leq 0$$.
ОДЗ: $$x^{2}+5x-14\neq 0$$
$$\left\{\begin{matrix}x_{1}+x_{2}\neq -5\\x_{1}\cdot x_{2}\neq-14\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}\neq-7\\x_{2}\neq 2\end{matrix}\right.$$
$$-\frac{14}{x^2 + 5x - 14} \leq 0$$$$\Leftrightarrow$$ $$(x+7)(x-2)>0$$
Начертим координатную прямую и отметим значения х , при которых знаменатель равен нулю (точки пустые согласно ОДЗ), расставим знаки, которые принимает выражение $$(x+7)(x-2)$$ на полученных промежутках:
Выберем промежутки, на которых выражение $$(x+7)(x-2)$$ принимает положительные значения: $$(-\infty; -7) \cup (2; +\infty)$$
Задание 21
Первый рабочий за час делает на $$8$$ деталей больше, чем второй, и выполняет заказ, состоящий из $$140$$ деталей, на $$2$$ часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
Пусть $$x$$ деталей в час - производительность первого, тогда $$x - 8$$ - второго. Тогда время выполнения заказа на $$140$$ деталей для первого $$t_1 = \frac{140}{x}$$ часов, для второго $$t_2 = \frac{140}{x - 8}$$. Получим:
$$\frac{140}{x - 8} - \frac{140}{x} = 2$$
$$140\left(\frac{1}{x - 8} - \frac{1}{x}\right) = 2$$
$$140 \cdot \frac{8}{x(x - 8)} = 2$$
$$1120 = 2x(x - 8)$$
$$x^2 - 8x - 560 = 0$$
$$D = 64 + 2240 = 2304$$
$$x = \frac{8 + 48}{2} = 28$$ деталей в час
$$x = \frac{8 - 48}{2} = -20$$ - не может быть, так как $$x > 0 $$ исходя из условия задачи.
Задание 22
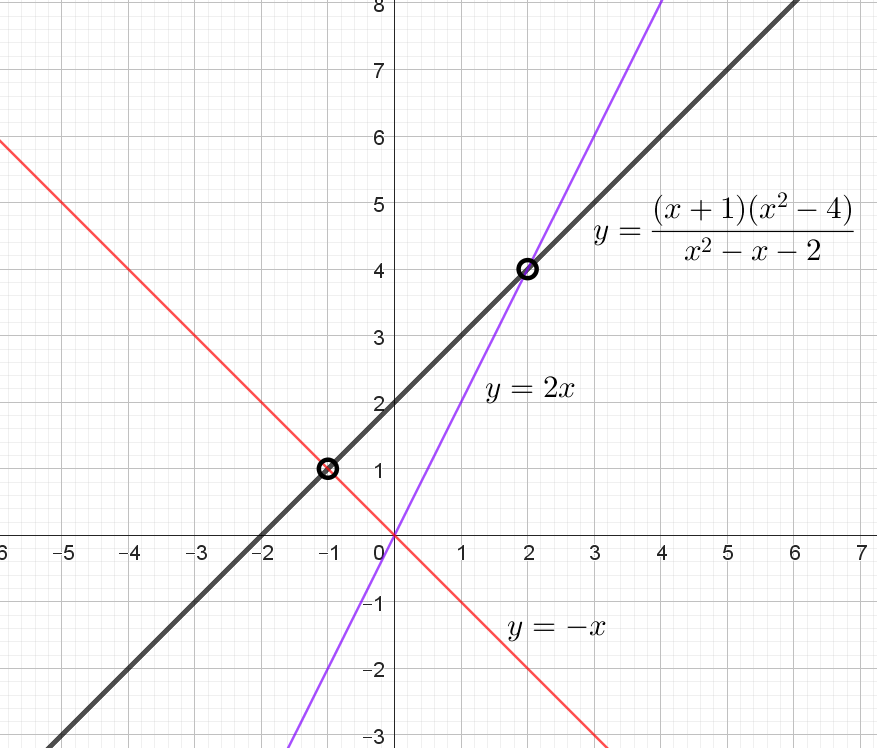
Постройте график функции $$y = \frac{(x+1)(x^2-4)}{x^2-x-2}$$
Определите, при каких значениях $$k$$ прямая $$y=kx$$ не имеет с графиком общих точек.
Разложим знаменатель на множители: $$x^2 - x - 2 = (x - 2)(x + 1)$$. Учтем, что $$x^2 - 4 = (x - 2)( x+ 2)$$
$$y = \frac{(x+1)(x-2)(x+2)}{(x-2)(x+1)} = x + 2$$ при $$x \neq -1; 2$$, так как знаменатель не может равнять нулю.
То есть графиком функции будет прямая $$y = x + 2$$, с учетом, что $$x \neq -1; y \neq -1+2 =1$$ и $$x \neq 2; y \neq 2 + 2 = 4$$
Пустые точки на графике: $$(-1; 1)$$, $$(2; 4)$$. На рисунке итоговая прямая выделена черным цветом.
Прямая $$y = kx$$ не имеет общих точек при:
Проходит через $$(-1; 1)$$ - выделена красным цветом. Подставим координаты данной точки в уравнение прямой: $$1 = k \cdot (-1) \Leftrightarrow k = -1$$
Проходит через $$(2; 4)$$ - выделена синим цветом. Подставим координаты данной точки в уравнение прямой: $$4 = k \cdot 2 \Leftrightarrow k = 2$$
Задание 23
Катет и гипотенуза прямоугольного треугольника равны $$24$$ и $$74$$. Найдите высоту, проведённую к гипотенузе.
По т. Пифагора второй катет: $$\sqrt{74^2 - 24^2} = \sqrt{5476 - 576} = \sqrt{4900} = 70$$
Найдем площадь, как половину произведения длин катетов: $$S = \frac{1}{2} \cdot 24 \cdot 70 = 840$$
С другой стороны, площадь можно вычислить, как половину произведения длин гипотенузы и высоты. Отсюда длина высоты: $$h = \frac{2S}{c} = \frac{1680}{74} = \frac{840}{37}$$
Задание 24
Точка $$E$$ — середина боковой стороны $$AB$$ трапеции $$ABCD$$, а $$EC = ED$$. Докажите, что трапеция $$ABCD$$ прямоугольная.
1) Пусть $$EH$$ - высота в треугольнике $$ECD$$, Тогда $$EH \perp CD$$.
2) Так как $$EC = ED$$, то треугольник $$ECD$$ - равнобедренный, тогда $$EH$$ - медиана. То есть $$H$$ - середина $$CD$$.
3) Тогда $$EH$$ - средняя линия трапеции $$ABCD$$, и $$EH \parallel AD \parallel BC$$.
4) Следовательно, $$BC\perp CD$$ и $$AD\perp CB$$, то есть трапеция - прямоугольная.
Задание 25
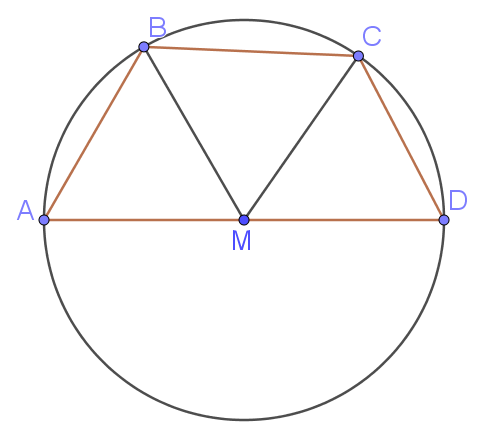
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$BC$$, если $$AD = 10$$, а углы $$C$$ и $$D$$ четырёхугольника равны соответственно $$110^\circ$$ и $$65^\circ$$.
1) $$MA = MB = MC = MD$$, следовательно, около $$ABCD$$ можно описать окружность с центром $$M$$. $$AD$$ - диаметр, $$AD = 10$$, $$MA = MB = MC = MD = 5$$
2) Угол $$C = 110^\circ$$, угол $$D = 65^\circ$$, тогда угол $$A = 180^\circ - 110^\circ = 70^\circ$$, угол $$B = 180^\circ - 65^\circ = 115^\circ$$
3) Треугольник $$AMB$$ - равнобедренный, тогда $$\angle ABM = \angle A = 70^\circ$$. Следовательно, $$\angle MBC = 115^\circ - 70^\circ = 45^\circ$$.
4) Треугольник $$BMC$$ - равнобедренный, тогда $$\angle MBC = \angle BCM = 45^\circ$$. Следовательно, $$\angle BMC = 180^\circ - 2\cdot 45^\circ = 90^\circ$$
5) По теореме косинусов: $$BC^2 = BM^2 + MC^2 - 2\cdot BM \cdot MC \cdot \cos BMC$$; $$BC = \sqrt{25 +25 - 2\cdot 25 \cdot 0} = \sqrt{50} = 5\sqrt{2}$$