Задание 130
Задание 130
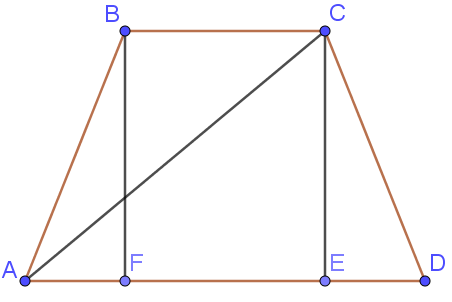
Диагональ равнобедренной трапеции образует с её основанием угол $$45^\circ$$. Найдите длину высоты трапеции, если её основания равны $$3$$ и $$4$$.
Пусть $$BF$$ и $$CE$$ - высоты. Тогда $$BCEF$$ - прямоугольник и $$BC = FE = 3$$
Треугольники $$ABF$$ и $$CED$$ - равны по катету и гипотенузе, тогда $$AF = \frac{AD-BC}{2} = 0,5$$
$$\angle CAE = 45^\circ$$, то есть треугольник $$AEC$$ - прямоугольный и равнобедренный, тогда $$CE = AE = 0,5 + 3 = 3,5$$
Аналоги к этому заданию:
Задание 109
Диагональ равнобедренной трапеции образует с её основанием угол $$45^\circ$$. Найдите длину высоты трапеции, если её основания равны $$4$$ и $$9$$.
Пусть $$BF$$ и $$CE$$ - высоты. Тогда $$BCEF$$ - прямоугольник и $$BC = FE = 4$$
Треугольники $$ABF$$ и $$CED$$ - равны по катету и гипотенузе, тогда $$AF = \frac{AD-BC}{2} = 2,5$$
$$\angle CAE = 45^\circ$$, то есть треугольник $$AEC$$ - прямоугольный и равнобедренный, тогда $$CE = AE = 2,5 + 4 = 6,5$$