ОГЭ 2021. Вариант 4. Ященко 36 вариантов ФИПИ школе.
Решаем 4 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 4 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Квартиры
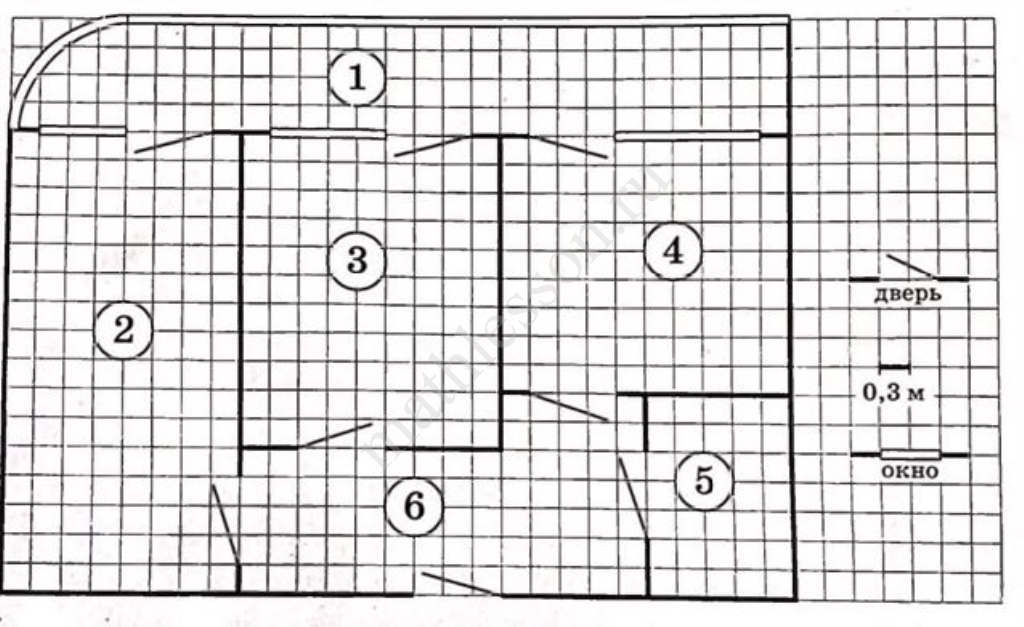
На рисунке изображён план двухкомнатной квартиры с панорамной лоджией в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна (и остекления лоджии), а также указано, что длина стороны клетки на плане соответствует 0,3 м. Вход в квартиру находится в прихожей. Самое большое по площади помещение — гостиная. В спальне, гостиной и кухне есть двери и окна, выходящие на лоджию, но в кухне окно шире, чем в других комнатах. Остекление лоджии со стороны гостиной закруглено. В квартире есть два помещения, в которых нет окон — это прихожая и санузел.
1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
| Помещения | гостиная | кухня | санузел | спальня | прихожая |
| Цифры |
2. Найдите радиус закругления остекления лоджии со стороны гостиной. Ответ дайте в сантиметрах.
3. Плитка для пола размером 15 см х 20 см продаётся в упаковках по 8 штук. Сколько упаковок плитки необходимо купить, чтобы выложить пол кухни?
4. На сколько процентов площадь кухни больше площади прихожей?
5. Найдите площадь лоджии. Считайте л равным 3,14. Ответ округлите до десятых квадратного метра.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\frac{1,8}{1+\frac{1}{11}}=$$$$\frac{18}{10}*\frac{11}{12}=$$$$\frac{33}{20}=1,65$$
Задание 8
Решите уравнение: $$(x + 20)( -x + 10) = 0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
При подготовке к экзамену Егор выучил $$16$$ билетов, а $$9$$ билетов не выучил. Найдите вероятность того, что ему попадётся выученный билет.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Закон Кулона можно записать в виде $$F = k \frac{q_1 q_2}{r^2}$$, где $$F$$ — сила взаимодействия зарядов (в ньютонах), $$q_1$$ и $$q_2$$ — величины зарядов (в кулонах), $$k$$ — коэффициент пропорциональности (в Н·м²/Кл²), а $$r$$ — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда $$q_1$$ (в кулонах), если $$k = 9 \cdot 10^9$$ Н·м²/Кл², $$q_2 = 0,004$$ Кл, $$r = 500$$ м, $$F = 1,008$$ Н.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Укажите решение системы неравенств:
$$\left\{\begin{aligned} x - 6,6 \ge 0 \\ x + 1 \ge 5 \end{aligned}\right.$$
1) $$[ 4;\ +\infty )$$
2) $$[ 4;\ 6,6 ]$$
3) $$[ 6,6;\ +\infty )$$
4) $$( -\infty;\ 4 ]$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
При проведении химического опыта реагент равномерно охлаждали на $$5,6^\circ\text{C}$$ в минуту. Найдите температуру реагента (в градусах Цельсия) спустя $$5$$ минут после начала проведения опыта, если начальная температура составляла $$+6,2^\circ\text{C}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В треугольнике $$ABC$$ угол $$A = 45^\circ$$, угол $$B = 60^\circ$$, $$BC = 4\sqrt{6}$$. Найдите $$AC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Решите уравнение: $$x(x^2 + 2x + 1) = 6(x + 1)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Заметим: $$x^2 + 2x + 1 = (x + 1)^2.$$ Тогда: $$x(x + 1)^2 = 6(x + 1).$$ Вынесем общий множитель: $$(x + 1)\bigl(x(x + 1) - 6\bigr) = 0.$$ Отсюда: $$x + 1 = 0,$$ или $$x(x + 1) - 6 = 0.$$
2) Первый корень: $$x = -1.$$
3) Решим квадратное уравнение: $$x^2 + x - 6 = 0.$$ Дискриминант: $$D = 1^2 - 4\cdot 1\cdot(-6) = 1 + 24 = 25,$$ $$x_{1,2} = \dfrac{-1 \pm \sqrt{25}}{2} = \dfrac{-1 \pm 5}{2}.$$ Получаем: $$x_1 = 2,\quad x_2 = -3.$$
Задание 19
Имеются два сосуда, содержащие $$30$$ кг и $$42$$ кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий $$40 \%$$ кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать $$37 \%$$ кислоты. Сколько процентов кислоты содержится во втором растворе?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 21
Высота $$AH$$ ромба $$ABCD$$ делит сторону $$CD$$ на отрезки $$DH=24$$ и $$CH=6$$. Найдите высоту ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Биссектриса $$CM$$ треугольника $$ABC$$ делит сторону $$AB$$ на отрезки $$AM=4$$ и $$MB=9$$. Касательная к окружности, описанной около треугольника $$ABC$$, проходит через точку $$C$$ и пересекает прямую $$AB$$ в точке $$D$$. Найдите $$CD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!