ОГЭ 2024. Вариант 9 Ященко 36 вариантов ФИПИ школе.
Решаем 9 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 9 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
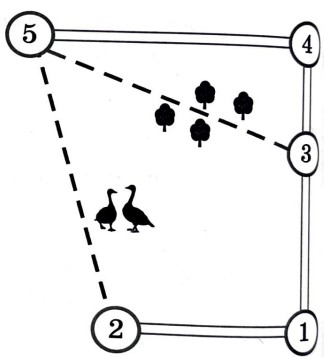
Миша летом отдыхает у дедушки и бабушки в деревне Анино. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Анино в Игнатьево можно проехать по шоссе до деревни Сосновка, где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Игнатьево через посёлок Дачный. Из Анино в Игнатьево можно проехать через посёлок Дачный и не заезжая в Сосновку, но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо птицефабрики до деревни Мальцево и там, повернув налево, по шоссе добраться до Игнатьево. По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке - 15 км/ч. Расстояние по шоссе от Анино до Сосновки равно 15 км, от Игнатьево до Сосновки - 24 км, от Игнатьево до Дачного -16 км, а от Игнатьево до Мальцево - 8 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр.
| Насел. пункты | д. Мальцево | с. Игнатьево | д. Сосновка | п. Дачный | д. Анино |
| Цифры |
2. На сколько процентов скорость, с которой едут Миша с дедушкой по тропинке, меньше их скорости по шоссе?
3. Найдите расстояние от деревни Анино до посёлка Дачного по лесной дорожке. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Сосновку?
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Миша с дедушкой, если поедут этим маршрутом.
Задание 13
Врач прописал больному капли по следующей схеме: в первый день $$5$$ капель, а в каждый следующий день — на $$5$$ капель больше, чем в предыдущий, до тех пор, пока дневная доза не достигнет $$20$$ капель. Такую дневную дозу ($$20$$ капель) больной ежедневно принимает неделю, а затем уменьшает приём на $$5$$ капель в день до последнего дня, когда больной принимает последние $$10$$ капель. Сколько пузырьков лекарства нужно купить на весь курс, если в каждом пузырьке $$5$$ мл лекарства, то есть $$150$$ капель?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Какое из следующих утверждений верно?
- Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
- В параллелограмме есть два равных угла.
- Площадь прямоугольного треугольника равна произведению длин его катетов.
В ответ запишите номер выбранного утверждения.
Задание 19
Решите систему уравнений: $$\left\{\begin{aligned} 2x^2 + y^2 = 36 \\ 8x^2 + 4y^2 = 36x \end{aligned}\right.$$
1) Левая часть второго уравнения равна четырёхкратной левой части первого: $$8x^2 + 4y^2 = 4(2x^2 + y^2).$$ Умножим первое уравнение на $$4$$: $$8x^2 + 4y^2 = 144.$$ Согласно второму уравнению: $$8x^2 + 4y^2 = 36x.$$ Приравниваем правые части: $$144 = 36x \;\Rightarrow\; x = 4.$$
2) Подставим $$x = 4$$ в первое уравнение: $$2\cdot 4^2 + y^2 = 36 \;\Rightarrow\; 32 + y^2 = 36 \;\Rightarrow\; y^2 = 4,$$ откуда $$y = 2$$ или $$y = -2.$$ Получаем решения $$(4;2)$$ и $$(4;-2).$$