ОГЭ 2022. Вариант 9 Ященко 36 вариантов ФИПИ школе.
Решаем 9 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 9 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
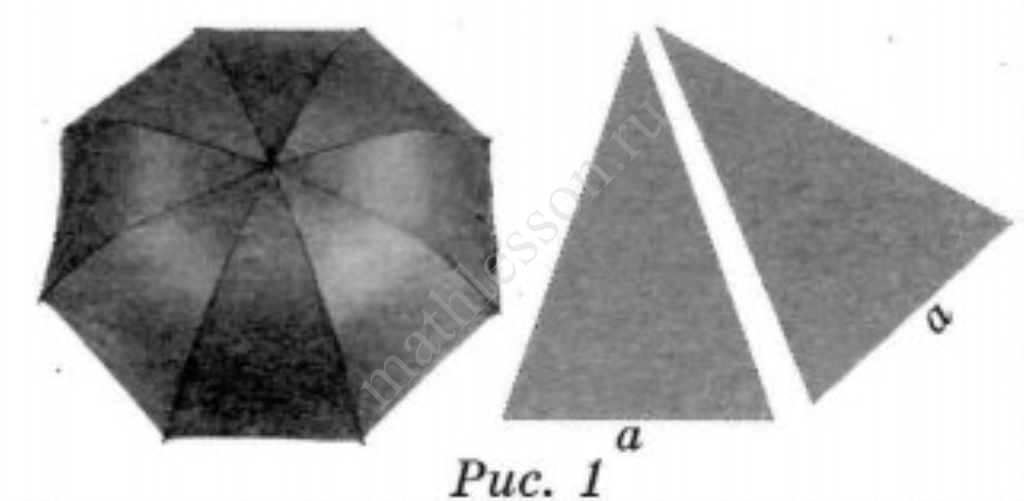
Зонты
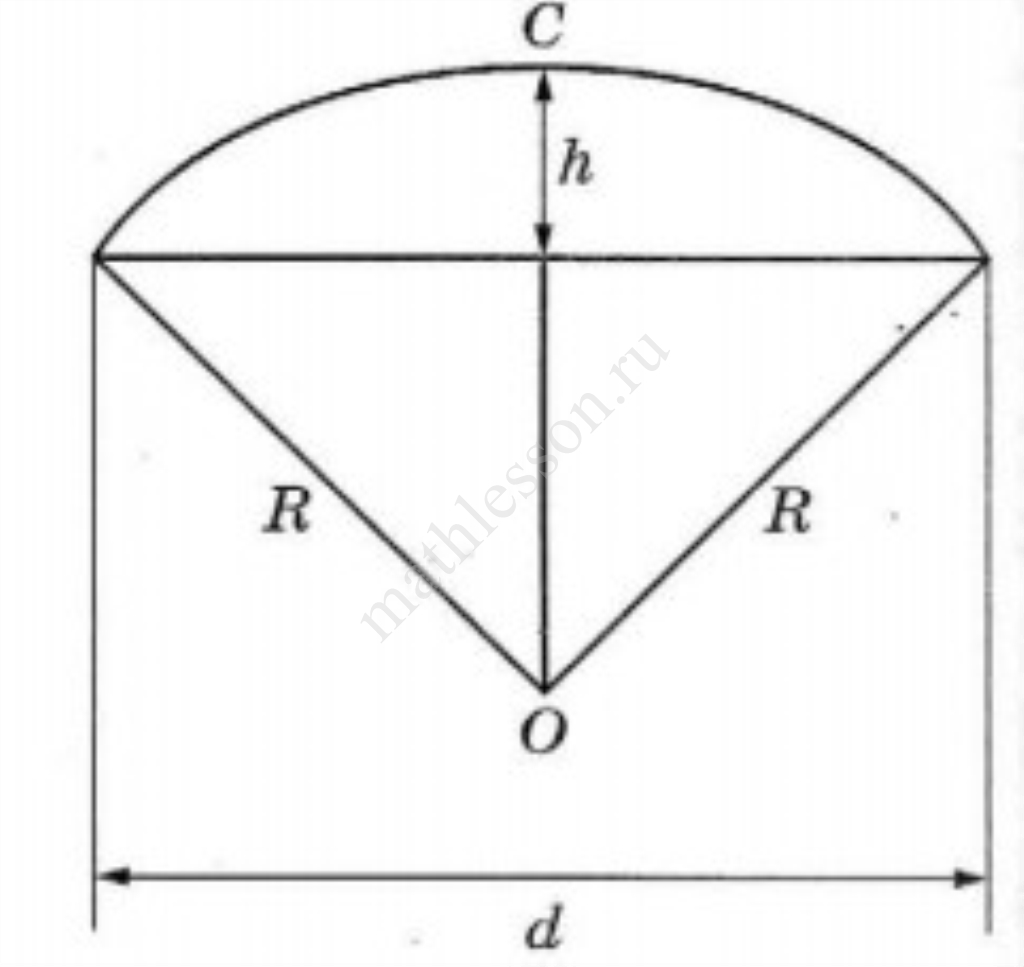
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц $$a$$. Оно оказалось равно $$38$$ см. Высота купола зонта $$h$$ (рис. 2) оказалась равна $$25$$ см, а расстояние $$d$$ между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно $$100$$ см.
1. Длина зонта в сложенном виде равна $$25$$ см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна $$6,2$$ см.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна $$53,1$$ см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$OC = R$$ (рис. 2). Ответ дайте в сантиметрах.
4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2\pi Rh$$, где $$R$$ — радиус сферы, a $$h$$ — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число $$\pi$$ округлите до $$3,14$$. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину $$35$$ м и ширину $$80$$ см. На фабрике из этого рулона были вырезаны треугольные клинья для $$29$$ зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь $$1050$$ кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Длина $$\frac{1}{3}$$ спицы: $$25-6,2=18,8$$ см. Тогда длина всей спины: $$3*18,8=56,4$$ см
2) Площадь одного треугольника $$S_1=\frac{1}{2} \cdot 38 \cdot 53,1=1008,9$$ см$$^{2}$$. Тогда площадь поверхности зонта: $$S_2=1008,9\cdot 8=8071,2$$ см$$^{2}$$.
3) Пусть x - высота равнобедреннего треугольника OMN. Тогда $$HN=50; ON=25+x.$$ По теореме Пифагора: $$x^{2}+2500=x^{2}+50x+625\to x=37,5\to R=37,5+25=62,5$$ см.
4) $$S=2\cdot 3,14\cdot 62,5\cdot 25=9812,5$$ см$$^{2}$$ $$\approx 9813$$ см$$^{2}$$.
5) Ушло на треугольники: $$29\cdot 8=1050=243600$$ см$$^{2}$$ $$=\frac{243600}{100\cdot 100}$$ м$$^{2}$$ $$=24,36$$ м$$^{2}$$. Площадь рулона: $$35\cdot 0,8=28$$ м$$^{2}$$ В обрезки пошло: $$\frac{28-24,36}{28}=100=13%$$
Задание 6
Найдите значение выражения: $$\frac{1}{5}-\frac{7}{25}:\frac{2}{7}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из следующих чисел заключено между числами $$-\frac{5}{17}$$ и $$-\frac{7}{19}$$?
1) $$-0,2$$
2) $$-0,3$$
3) $$-0,4$$
4) $$-0,5$$
В ответ запишите номер выбранного варианта.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\frac{5^9 \cdot 9^6}{45^6}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$ \frac{5^9 \cdot 9^6}{45^6}=\frac{5^9 \cdot 9^6}{(5 \cdot 9)^6}=$$$$\frac{5^9 \cdot 9^6}{5^{6 \cdot 9^6}}=5^{9-6}=5^3=125$$
Задание 9
Найдите корень уравнения: $$2x^2 = 9x$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В девятом физико-математическом классе учатся $$13$$ мальчиков и $$7$$ девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Скорость камня (в м/с), падающего с высоты $$h$$ (в м), в момент удара о землю можно найти по формуле $$v = \sqrt{2gh}$$. Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты $$40$$ м. Считайте, что ускорение свободного падения $$g$$ равно $$9,8$$ м/с².
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
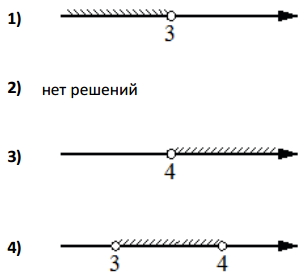
Укажите решение системы неравенств:
$$\left\{\begin{aligned} -9 + 3x 0 \\ 2 - 3x -10 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\left\{\begin{matrix}-9+3x< 0\\2-3x< -10\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}3x< 9\\-3x< -12\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x< 3\\x> 4\end{matrix}\right.$$
Задание 14
Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает $$13$$ метров, а в каждую следующую секунду — на $$10$$ метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Хорды $$AC$$ и $$BD$$ окружности пересекаются в точке $$P$$, $$BP = 9$$, $$CP = 15$$, $$DP = 20$$. Найдите $$AP$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Диагонали $$AC$$ и $$BD$$ трапеции $$ABCD$$ с основаниями $$BC$$ и $$AD$$ пересекаются в точке $$O$$, $$BC = 6$$, $$AB = 13$$, $$AC = 38$$. Найдите $$AO$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Боковые стороны любой трапеции равны.
- Площадь прямоугольника равна произведению длин его смежных сторон.
- Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$\frac{1}{(x - 3)^2} - \frac{3}{x - 3} - 4 = 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Сделаем замену: $$t = \frac{1}{x - 3}.$$ Получим квадратное уравнение: $$t^2 - 3t - 4 = 0.$$
2) Дискриминант: $$D = (-3)^2 - 4\cdot 1\cdot(-4) = 9 + 16 = 25,$$ $$t_{1,2} = \dfrac{3 \pm 5}{2}.$$ То есть: $$t_1 = 4,\qquad t_2 = -1.$$
3) Возвращаемся к $$x$$:
1) $$\frac{1}{x - 3} = 4,$$ $$x - 3 = \frac{1}{4},$$ $$x = \frac{13}{4} = 3{,}25.$$
2) $$\frac{1}{x - 3} = -1,$$ $$x - 3 = -1,$$ $$x = 2.$$
Задание 21
Велосипедист выехал с постоянной скоростью из города $$A$$ в город $$B$$, расстояние между которыми равно $$209$$ км. На следующий день он отправился обратно в $$A$$, увеличив скорость на $$8$$ км/ч. По пути он сделал остановку на $$8$$ часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из $$A$$ в $$B$$. Найдите скорость велосипедиста на пути из $$B$$ в $$A$$.
Задание 22
Постройте график функции $$y = \frac{(x^2 + x - 6)(x^2 - 2x - 3)}{x^2 - 9}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Биссектрисы углов $$A$$ и $$B$$ при боковой стороне $$AB$$ трапеции $$ABCD$$ пересекаются в точке $$F$$. Найдите $$AB$$, если $$AF=21$$, $$BF=20$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
Точки $$M$$ и $$N$$ лежат на стороне $$AC$$ треугольника $$ABC$$ на расстояниях соответственно $$9$$ и $$11$$ от вершины $$A$$. Найдите радиус окружности, проходящей через точки $$M$$ и $$A$$ и касающейся луча $$AB$$, если $$\cos \angle BAC=\frac{\sqrt{11}}{6}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!