ОГЭ 2022. Вариант 3 Ященко 36 вариантов ФИПИ школе.
Решаем 3 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 3 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
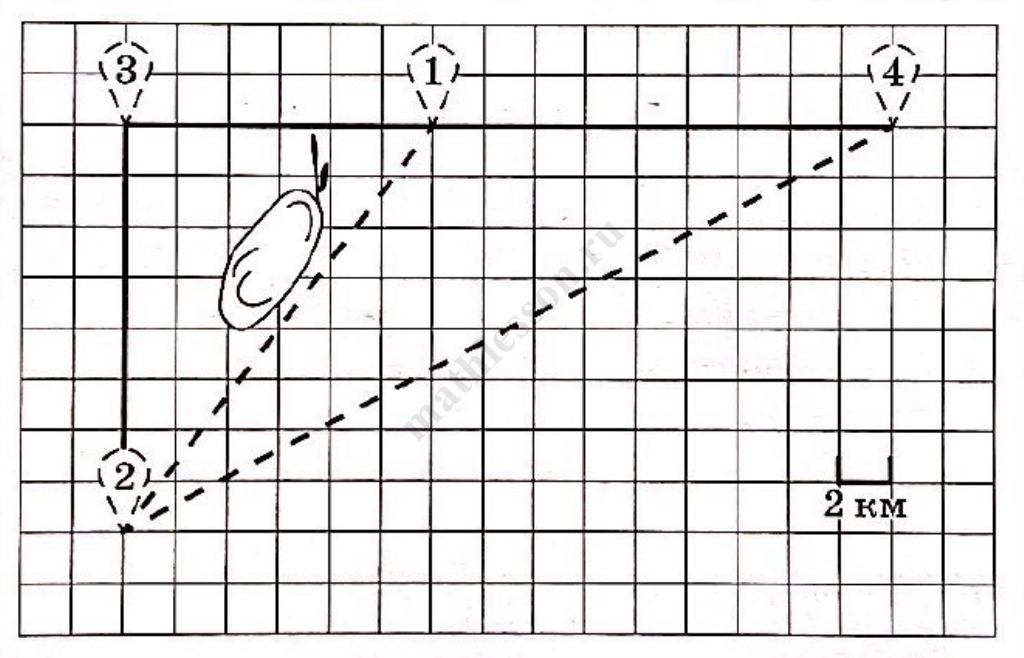
План местности
Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево до деревни Рябиновки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут: в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
1) Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Насел. пункты | д. Пирожки | с. Княжеское | д. Рябиновка |
| Цифры |
2) Сколько километров проедут Серёжа с папой от деревни Пирожки до села Княжеское, если они поедут по шоссе через деревню Рябиновку?
3) Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.
4) Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут по прямой грунтовой дороге?
5) В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеском, деревне Васильево и деревне Рябиновке.
| Наименование продукта | д. Пирожки | с. Княжеское | д. Васильево | д. Рябиновка |
| Молоко (1 л) | 48 | 45 | 50 | 52 |
| Хлеб (1 батон) | 34 | 32 | 33 | 28 |
| Сыр «Российский» (1 кг) | 240 | 280 | 270 | 260 |
| Говядина (1 кг) | 370 | 400 | 380 | 420 |
| Картофель (1 кг) | 22 | 16 | 28 | 30 |
Серёжа с папой хотят купить 2 л молока, 3 батона хлеба и 1 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На тарелке лежат одинаковые на вид пирожки: $$13$$ с мясом, $$11$$ с капустой и $$6$$ с вишней. Антон наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более $$5$$ минут рассчитывается по формуле $$C = 170 + 15 \cdot (t - 5)$$, где $$t$$ — длительность поездки (в минутах). Пользуясь этой формулой, рассчитайте стоимость $$14$$-минутной поездки. Ответ дайте в рублях.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
У Яны есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту $$240$$ см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше $$5$$ см?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$BC = 7$$, $$AC = 35$$. Найдите $$\tan B$$.
Задание 16
Угол $$A$$ трапеции $$ABCD$$ с основаниями $$AD$$ и $$BC$$, вписанной в окружность, равен $$52^\circ$$. Найдите угол $$B$$ этой трапеции. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Две стороны параллелограмма равны $$6$$ и $$17$$, а один из углов этого параллелограмма равен $$30^\circ$$. Найдите площадь этого параллелограмма.
Задание 19
Какие из следующих утверждений верны?
- Все высоты равностороннего треугольника равны.
- Существуют три прямые, которые проходят через одну точку.
- Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Перенесём всё в левую часть: $$(4x - 7)^2 - (7x - 4)^2 \ge 0,$$ $$(4x - 7 - (7x - 4))(4x - 7 + (7x - 4)) \ge 0.$$ Получаем $$(-3x - 3)(11x - 11) \ge 0,$$ или $$-33(x + 1)(x - 1) \ge 0.$$
2) Поделим на $$-33$$ и меняем знак неравенства: $$(x + 1)(x - 1) \le 0.$$ Корни: $$x_1 = -1,\; x_2 = 1.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x + 1)(x - 1)$$ на полученных интервалах:
Выражение неположительно: $$x \in [-1; 1].$$
Задание 21
Из $$A$$ в $$B$$ одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью $$30$$ км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на $$9$$ км/ч, в результате чего прибыл в $$B$$ одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Задание 22
Постройте график функции $$y = \left\{\begin{aligned} x^2 - 8x + 14, & x \geq 0; \\ x - 2, & x < 3 \end{aligned}\right.$$ Определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Задание 23
Прямая пересекает стороны $$AB$$ и $$BC$$ треугольника $$ABC$$ в точках $$K$$ и $$N$$ соответственно. Известно, что $$AB=CN=16$$, $$BC=20$$, $$AC=28$$, $$AK=11$$. Найдите длину отрезка $$KN$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
В выпуклом четырёхугольнике $$ABCD$$ углы $$CDB$$ и $$CAB$$ равны. Докажите, что углы $$BCA$$ и $$BDA$$ также равны.
Задание 25
Найдите площадь трапеции, диагонали которой равны $$10$$ и $$8$$, а средняя линия равна $$3$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- Проведем из точки $$C$$ прямую, параллельную $$BD$$, пусть она пересекает $$AD$$ в точке $$K$$.
- $$BC\parallel DK ; BD\parallel CK \Rightarrow BCKD-$$ параллелограмм и $$BC=DK$$, $$BD=CK$$, $$AK=AD+DK=AD+BC$$.
- $$AD+BC=3\cdot 2=6$$ (удвоенная средняя линия)
- Пусть $$CH\perp AD: S_{ABCD}=\frac{BC+AD}{2} \cdot CH=\frac{1}{2} \cdot AK \cdot CH=S_{ACK}$$.
- $$p_{ACK}=\frac{10+8+6}{2}=12$$ По формуле Герона: $$S_{ACK}=\sqrt{12(12-10)(12-8)(12-6)}=\sqrt{12 \cdot 2 \cdot 4 \cdot 6}=\sqrt{12^2 \cdot 2^2}=24$$