ОГЭ 2021. Вариант 27 Ященко 36 вариантов ФИПИ школе.

На координатной прямой отмечены числа $$a$$ и $$b$$. Какое из приведённых утверждений для этих чисел верно?
1) $$a + b 0$$
2) $$a - b > 0$$
3) $$ab 0$$
4) $$ab^2 > 0$$

Найдите значение выражения $$\frac{(a^5)^3 \cdot a^6}{a^{22}}$$ при $$a = 2$$.

Решите уравнение: $$( -x - 4 )( 3x + 3 ) = 0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.

В сборнике билетов по физике всего $$40$$ билетов, в $$6$$ из них встречается вопрос по теме «Термодинамика». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Термодинамика».

На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между знаками коэффициентов $$a$$ и $$c$$ и графиками функций.

Коэффициенты
А. $$a > 0$$; $$c < 0$$
Б. $$a > 0$$; $$c > 0$$
В. $$a < 0$$; $$c > 0$$

ГРАФИКИ

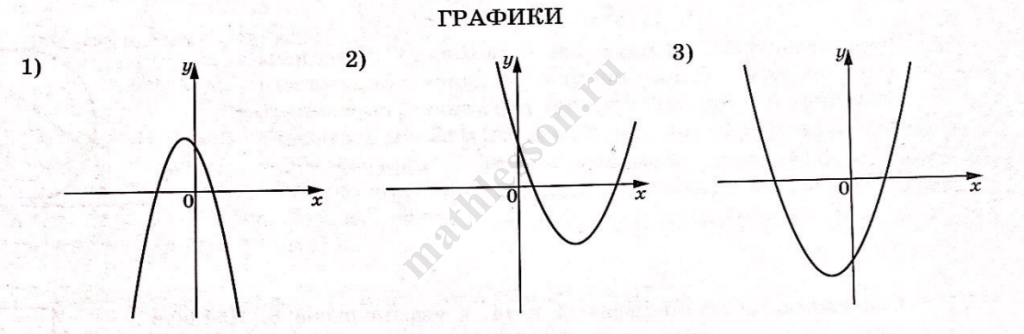
В таблице под каждой буквой укажите соответствующий номер.

Площадь прямоугольника вычислить по формуле $$S = \frac{d^2 \sin \alpha}{2}$$, где $$d$$ — длина диагонали, $$\alpha$$ — угол между диагоналями. Пользуясь этой формулой, найдите площадь $$S$$, если $$d = 3$$ и $$\sin \alpha = \frac{2}{3}$$.

Укажите неравенство, решение которого изображено на рисунке:
1) $$x^2 - 1 \ge 0$$
2) $$x^2 - x \ge 0$$
3) $$x^2 - 1 \le 0$$
4) $$x^2 - x \le 0$$

Каждое простейшее одноклеточное животное — инфузория-туфелька — размножается делением на $$2$$ части. Сколько инфузорий было первоначально, если после четырёхкратного деления их стало $$640$$?

Два катета прямоугольного треугольника равны $$7$$ и $$12$$. Найдите его площадь.

Окружность с центром в точке $$O$$ описана около равнобедренного треугольника $$ABC$$, в котором $$AB = BC$$ и $$\angle ABC = 107^\circ$$. Найдите величину угла $$BOC$$. Ответ дайте в градусах.

Высота равнобедренной трапеции, проведённая из вершины $$C$$, делит основание $$AD$$ на отрезки длиной $$14$$ и $$19$$. Найдите длину основания $$BC$$.

На клетчатой бумаге с размером клетки $$1 \times 1$$ изображена фигура. Найдите её площадь.

Какое из следующих утверждений верно?

1. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2. Основания равнобедренной трапеции равны.
3. Все высоты равностороннего треугольника равны.

В ответе запишите номер выбранного утверждения.

Решите неравенство: $$(3x - 7)^2 \geq (5x - 9)^2$$

Смешали $$4$$ литра $$35$$ - процентного раствора вещества с $$11$$ литрами $$5$$ - процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Постройте график функции $$y = \left\{\begin{aligned} x^2 + 2x + 1, & x \ge -2 \\ x + 3, & x -2 \end{aligned}\right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.

Точка $$H$$ является основанием высоты, проведённой из вершины прямого угла $$B$$ треугольника $$ABC$$ к гипотенузе $$AC$$. Найдите $$AB$$, если $$AH=3$$, $$AC=27$$.

На средней линии трапеции $$ABCD$$ с основаниями $$AD$$ и $$BC$$ выбрали произвольную точку $$E$$. Докажите, что сумма площадей треугольников $$BEC$$ и $$AED$$ равна половине площади трапеции.

Четырёхугольник $$ABCD$$ со сторонами $$AB=12$$ и $$CD=30$$ вписан в окружность. Диагонали $$AC$$ и $$BD$$ пересекаются в точке $$K$$, причём $$\angle AKB=60^{\circ}$$. Найдите радиус окружности, описанной около этого четырёхугольника.