ОГЭ 2022. Вариант 17 Ященко 36 вариантов ФИПИ школе.
Решаем 17 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 17 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
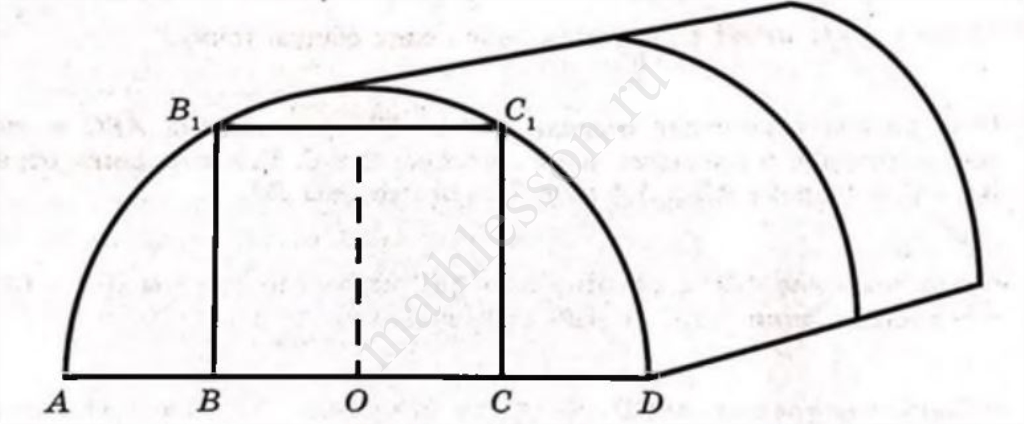
Теплицы
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки В, О и С делят отрезок АО на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
1. Какое количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 6
Задание 7
На координатной прямой отмечены числа $$x$$, $$y$$ и $$z$$. Какая из разностей $$x-y$$, $$y-z$$, $$z-x$$ положительна?
1) $$x - y$$
2) $$y - z$$
3) $$z - x$$
4) ни одна из них
Учтем, что в порядке возрастания числа расположатся следующим образом: $$z,x,y$$. Тогда:
- x-y<0
- y-z>0
- z-x<0
- ни одна из них
Как видим, положительным будет только второй вариант ответа
Задание 8
Найдите значение выражения $$\frac{3^{-7} \cdot 3^2}{3^{-9}}$$
Задание 9
Решите уравнение: $$x^2 - 20 = x$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
$$x^{2}-20=x\Leftrightarrow$$$$x^{2}-x-20=0$$
По теореме Виетта сумма корней равна 1, произведение -20. Следовательно, корни равны 5 и -4. В ответ необходимо указать больший, то есть 5
Задание 10
Вероятность того, что новый фен прослужит больше года, равна $$0,98$$. Вероятность того, что он прослужит больше двух лет, равна $$0,86$$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Задание 11
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между графиками функций и знаками коэффициентов $$a$$ и $$c$$.
Коэффициенты
1. $$a > 0$$, $$c > 0$$
2. $$a > 0$$, $$c < 0$$
3. $$a < 0$$, $$c > 0$$
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Коэффициент а отвечает за направление ветвей параболы и расширение/сужение графика относительно оси Оу (если а>0 - ветви вверх, а<0 - вниз).
Коэффициент с за пересечение оси Оу графиком функции (если с>0, то пересечение над осью Ох, с<0 - под осью)
Тогда получим:
Задание 12
Работа постоянного тока (в джоулях) вычисляется по формуле $$A = \frac{U^2 t}{R}$$, где $$U$$ — напряжение (в вольтах), $$R$$ — сопротивление (в омах), $$t$$ — время (в секундах). Пользуясь этой формулой, найдите $$A$$ (в джоулях), если $$t = 9$$ с, $$U = 8$$ В и $$R = 12$$ Ом.
Подставим значения с условия задания: $$A=\frac{U^{2}t}{R}=\frac{8^{2}\cdot 9}{12}=48$$
Задание 13
Укажите решение неравенства: $$-3 - 5x \le x + 3$$
1) $$( -\infty;\ 0 ]$$
2) $$[ -1;\ +\infty )$$
3) $$[ 0;\ +\infty )$$
4) $$( -\infty;\ -1 ]$$
Задание 14
В $$11:00$$ часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В $$21:00$$ того же дня часы отставали на $$20$$ минут. На сколько минут отставали часы спустя $$24$$ часа после того, как они сломались?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 14$$, $$AB = 20$$. Найдите $$\sin B$$.
Задание 16
Отрезки $$AC$$ и $$BD$$ — диаметры окружности с центром $$O$$. Угол $$ACB$$ равен $$63^\circ$$. Найдите угол $$AOD$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
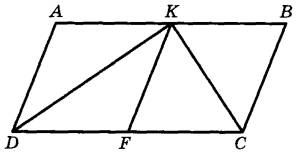
Площадь параллелограмма $$ABCD$$ равна $$92$$. Точка $$E$$ — середина стороны $$AB$$. Найдите площадь трапеции $$DAEC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 18
На клетчатой бумаге с размером клетки $$1 \times 1$$ изображён треугольник $$ABC$$. Найдите длину его медианы, проведённой из вершины $$C$$.
Задание 19
Какие из следующих утверждений верны?
- Площадь треугольника меньше произведения двух его сторон.
- Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
- Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
- Верно, так как по формуле она равна половине произведения двух смежных сторон на синус угла между ними, а синус угла всегда не больше единицы
- Нет, равен его половине
- Верно, и при том только одну
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Перенесём всё в одну часть и применим формулу разности квадратов: $$x^4 - (2x - 3)^2 = 0,$$ $$(x^2 - (2x - 3))(x^2 + (2x - 3)) = 0,$$ $$(x^2 - 2x + 3)(x^2 + 2x - 3) = 0.$$
2) Решим квадратные уравнения.
Уравнение $$x^2 - 2x + 3 = 0.$$ Дискриминант: $$D = (-2)^2 - 4\cdot 1\cdot 3 = 4 - 12 = -8.$$ Действительных корней нет.
Уравнение $$x^2 + 2x - 3 = 0.$$ Дискриминант: $$D = 2^2 - 4\cdot 1\cdot(-3) = 4 + 12 = 16.$$ Корни: $$x_{1,2} = \dfrac{-2 \pm \sqrt{16}}{2\cdot 1} = \dfrac{-2 \pm 4}{2},$$ $$x_1 = 1,\quad x_2 = -3.$$
Задание 21
Моторная лодка прошла против течения реки $$132$$ км и вернулась в пункт отправления, затратив на обратный путь на $$5$$ часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна $$5$$ км/ч.
Пусть скорость лодки х км/ч. Тогда скорость против течения будет х-5 км/ч. а по течению х+5 км/ч
По условию на обратный путь затрачено на 5 часов меньше, тогда: $$\frac{132}{x-5}-\frac{132}{x+5}=5$$
Приведем к общему знаменателю: $$\frac{132(x+5)-132(x-5)}{x^2-25}=5$$
Задание 22
Постройте график функции $$y = x^2 + 3x - 3|x + 2| + 2$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 23
Прямая пересекает стороны $$AB$$ и $$BC$$ треугольника $$ABC$$ в точках $$K$$ и $$N$$ соответственно. Известно, что $$AB=12$$, $$BC=15$$, $$AC=24$$, $$AK=7$$, $$CN=11$$. Найдите длину отрезка $$KN$$.
- ВК=АВ-АК=12-7=5
- ВN=ВС-ВN=15-11=4
- Рассмотрим треугольники АВС и КВN. Угол В общий АВ/ВN=BC/BK, т.к.12/4 =15/5 =3 Следовательно данные треугольники подобны по двум сторонам и углу между ними, причем коэффициент подобия равен 3.
- Поэтому и АС/КN =3, т.е. 24/КN =3, т.е. КN=8
Задание 24
Сторона $$AB$$ параллелограмма $$ABCD$$ вдвое больше стороны $$AD$$. Точка $$K$$ - середина стороны $$AB$$. Докажите, что $$DK$$ - биссектриса угла $$ADC$$.
Проведём FK параллельно AD (см. рисунок). Тогда AD = AK = KB. Следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD делит угол ADC пополам.
