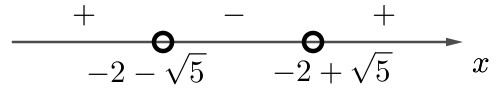ОГЭ 2021. Вариант 6. Ященко 36 вариантов ФИПИ школе.
Решаем 6 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 6 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе — через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое. Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки ДО Николаевки равно 12 км, от Марьевки ДО Запрудья - 20 км, а от Запрудья до Соснового 15 км.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Насел. пункты | с. Сосновое | д. Запрудье | д. Марьевка | д. Николаевка |
| Цифры |
Задание 2.
На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Задание 3.
Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Задание 4.
Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Задание 5.
Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\sqrt{0,25m^6n^4}$$, при $$m = 3$$ и $$n = 4$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В лыжных гонках участвуют $$13$$ спортсменов из России, $$2$$ — из Норвегии и $$5$$ — из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Закон Джоуля–Ленца можно записать в виде $$Q = I^2 R t$$, где $$Q$$ — количество теплоты (в джоулях), $$I$$ — сила тока (в амперах), $$R$$ — сопротивление цепи (в омах), а $$t$$ — время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи $$R$$ (в омах), если $$Q = 1152$$ Дж, $$I = 8$$ А, $$t = 6$$ с.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$(x+3)(x-6)>0$$
- $$(6;+\infty)$$
- $$(-3;+\infty)$$
- $$(-\infty;-3);(6;+\infty)$$
- $$(-3;6)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В амфитеатре $$30$$ рядов. В первом ряду $$12$$ мест, а в каждом следующем — на $$2$$ места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Точки $$M$$ и $$N$$ являются серединами сторон $$AB$$ и $$BC$$ треугольника $$ABC$$ соответственно. Отрезки $$AN$$ и $$CM$$ пересекаются в точке $$O$$, $$AN = 33$$, $$CM = 15$$. Найдите $$ON$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений неверно ?
- Сумма острых углов прямоугольного треугольника равна $$90^{\circ}$$ градусам.
- Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
- Любые два равносторонних треугольника подобны.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


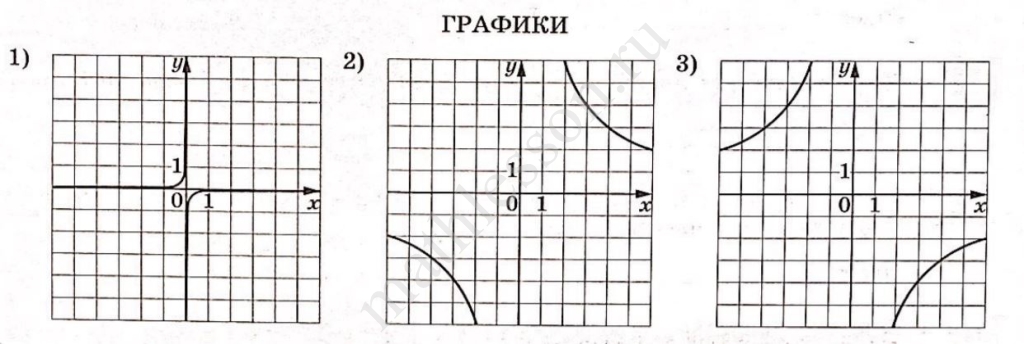
Задание 20
Решите неравенство: $$\frac{-16}{(x+2)^2 - 5} \le 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Числитель $$-16$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была отрицательной, знаменатель должен быть положительным: $$(x+2)^2 - 5 > 0.$$
2) Решим неравенство: $$(x+2)^2 - 5 > 0.$$ Учтем, что $$(x+2)^2 - 5 = (x + 2)^2 - (\sqrt{5})^2 = (x+2-\sqrt{5})(x+2+\sqrt{5}).$$ Нули $$x_1 = -2 - \sqrt{5}; x_2 = -2 + \sqrt{5}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x+2-\sqrt{5})(x+2+\sqrt{5})$$ на полученных промежутках:
Выражение положительное при: $$x \in (-\infty;\,-2-\sqrt{5}) \;\cup\; (-2+\sqrt{5};\,+\infty).$$
Задание 21
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на $$28$$ минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет $$286$$ км, скорость первого велосипедиста равна $$10$$ км/ч, скорость второго — $$30$$ км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
В параллелограмме $$ABCD$$ проведена диагональ $$AC$$. Точка $$O$$ является центром окружности, вписанной в треугольник $$ABC$$. Расстояния от точки $$O$$ до точки $$A$$ и прямых $$AD$$ и $$AC$$ соответственно равны $$25$$, $$13$$ и $$7$$. Найдите площадь параллелограмма $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!