ОГЭ 2021. Вариант 20 Ященко 36 вариантов ФИПИ школе.
Решаем 20 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 19 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Теплицы
Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25 х 25 см. Высота теплицы показана на рисунке отрезком HF.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах. Результат округлите до десятков.
5. Сколько квадратных метров плёнки необходимо купить для передней и задней стенок, если с учётом крепежа её нужно брать с запасом 15% ? Ответ округлите до десятых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Найдите значение выражения $$\frac{b^7 \cdot b^{16}}{b^{21}}$$ при $$b = 9$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Решите уравнение: $$\frac{1}{3}x^2 - 27 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
В среднем из $$150$$ карманных фонариков, поступивших в продажу, $$6$$ — неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Площадь четырёхугольника можно вычислить по формуле $$S = \frac{1}{2} d_1 d_2 \sin \alpha$$, где $$d_1$$ и $$d_2$$ — длины диагоналей четырёхугольника, $$\alpha$$ — угол между диагоналями. Пользуясь этой формулой, найдите площадь $$S$$, если $$d_1 = 4$$, $$d_2 = 18$$, $$\sin \alpha = \frac{8}{9}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Укажите неравенство, которое не имеет решений:
1) $$x^2 + 15 \ge 0$$
2) $$x^2 - 15 \le 0$$
3) $$x^2 - 15 \ge 0$$
4) $$x^2 + 15 \le 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
При проведении химического опыта реагент равномерно охлаждали на $$6,5^\circ\text{C}$$ в минуту. Найдите температуру реагента (в градусах Цельсия) спустя $$4$$ минуты после начала проведения опыта, если начальная температура составляла $$-4,9^\circ\text{C}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В треугольнике $$ABC$$ $$AC = 55$$, $$BM$$ — медиана, $$BM = 36$$. Найдите $$AM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Диагональ $$BD$$ параллелограмма $$ABCD$$ образует с его сторонами углы, равные $$65^\circ$$ и $$50^\circ$$. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


| $$\angle B=65+50=115^{\circ}$$ $$\angle A=180^{\circ}-\angle B=180^{\circ}-115^{\circ}=65^{\circ}$$ |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Какое из следующих утверждений верно?
- Диагонали прямоугольной трапеции равны.
- Существует прямоугольник, диагонали которого взаимно перпендикулярны.
- В тупоугольном треугольнике все углы тупые.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Числитель $$-12$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была отрицательной, знаменатель должен быть положительным: $$4 + 3x - x^2 > 0.$$
2) Решим неравенство: $$4 + 3x - x^2 > 0.$$ Перенесём всё в одну сторону: $$-x^2 + 3x + 4 > 0 \;\Longleftrightarrow\; x^2 - 3x - 4 < 0.$$ Учтём, что $$x^2 - 3x - 4 = (x-4)(x+1).$$ Нули: $$x_1 = -1;\quad x_2 = 4.$$ Отметим их на координатной прямой и расставим знаки, которые принимает выражение $$(x-4)(x+1)$$ на полученных промежутках.
Выражение отрицательное при: $$x \in (-1;\,4).$$
Задание 20
В сосуд, содержащий $$9$$ литров $$16$$ - процентного водного раствора вещества, добавили $$3$$ литра воды. Сколько процентов составляет концентрация получившегося раствора?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 21
Постройте график функции $$y = |x^2 + x - 2|$$. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Найдите боковую сторону $$AB$$ трапеции $$ABCD$$, если углы $$ABC$$ и $$BCD$$ равны соответственно $$30^{\circ}$$ и $$120^{\circ}$$, a $$CD=25$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


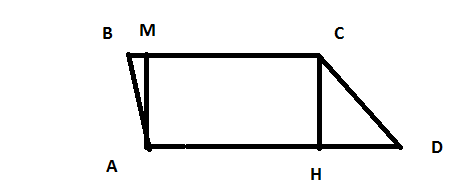
$$D=180-C=180-120=60$$
Из CHB : $$CH=CD * \sin D = 25 \sin 60=25 * \frac{\sqrt{3}}{2}=\frac{25\sqrt{3}}{2}$$
$$AM=CH$$ ;
$$AB=\frac{AM}{\sin B}=\frac{\frac{25\sqrt{3}}{2}}{\frac{1}{2}}=25\sqrt{3}$$
Задание 23
Внутри параллелограмма $$ABCD$$ выбрали произвольную точку $$E$$. Докажите, что сумма площадей треугольников $$AEB$$ и $$CED$$ равна половине площади параллелограмма.
Проведём через точку $$E$$ прямую $$MN \parallel AB$$
Площадь $$\triangle ABE = \frac{1}{2}S_{ABNM}$$ (*)
(*) Докажем это утверждение. Пусть $$EH$$ - высота в треугольнике $$ABE$$. Тогда $$S_{ABE} = \frac{1}{2} \cdot AB \cdot EH$$. Но $$S_{ABNM} = AB \cdot EH$$. Тогда $$S_{ABE}=\frac{1}{2}S_{ABNM}$$.Площадь $$\triangle CED = \frac{1}{2}S_{CNMD}$$
Сумма площадей: $$S_{ABE} + S_{CED} = \frac{1}{2}(S_{ABNM} + S_{CNMD})$$
Но $$S_{ABNM} + S_{CNMD} = S_{ABCD}$$
Таким образом: $$S_{ABE} + S_{CED} = \frac{1}{2}S_{ABCD}$$
Что и требовалось доказать.
Задание 24
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$AD$$, если $$BC=19$$, а углы $$B$$ и $$C$$ четырёхугольника равны соответственно $$95^{\circ}$$ и $$115^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!