ОГЭ 2021. Вариант 11 Ященко 36 вариантов ФИПИ школе.
Решаем 11 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 11 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Листы
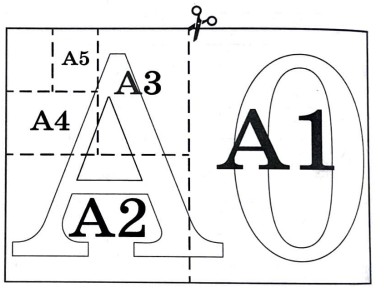
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: A0, A1, А2 и так далее. Площадь листа формата АО равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата A1. Если так же лист A1 разрезать пополам, получаются два листа формата А2 и так далее.
Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны. друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится). На практике размеры листа округляются до целого числа миллиметров. В таблице 1 даны размеры листов бумаги четырёх форматов: от А3 до А6.
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 210 | 297 |
| 2 | 297 | 420 |
| 3 | 105 | 148 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов А6, А5, А4 и А3 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А6 | А5 | А4 | Ф3 |
2. Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата A0?
3. Найдите длину меньшей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата А5. Ответ дайте в квадратных сантиметрах.
5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$a^{-13} \cdot (a^5)^3$$ при $$a = 7$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Найдите решение уравнения: $$2x^2 + 5x - 7 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в $$4$$ раза меньше, чем с зелёным. Найдите вероятность того, что случайно выбранный пакетик окажется с зелёным чаем.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


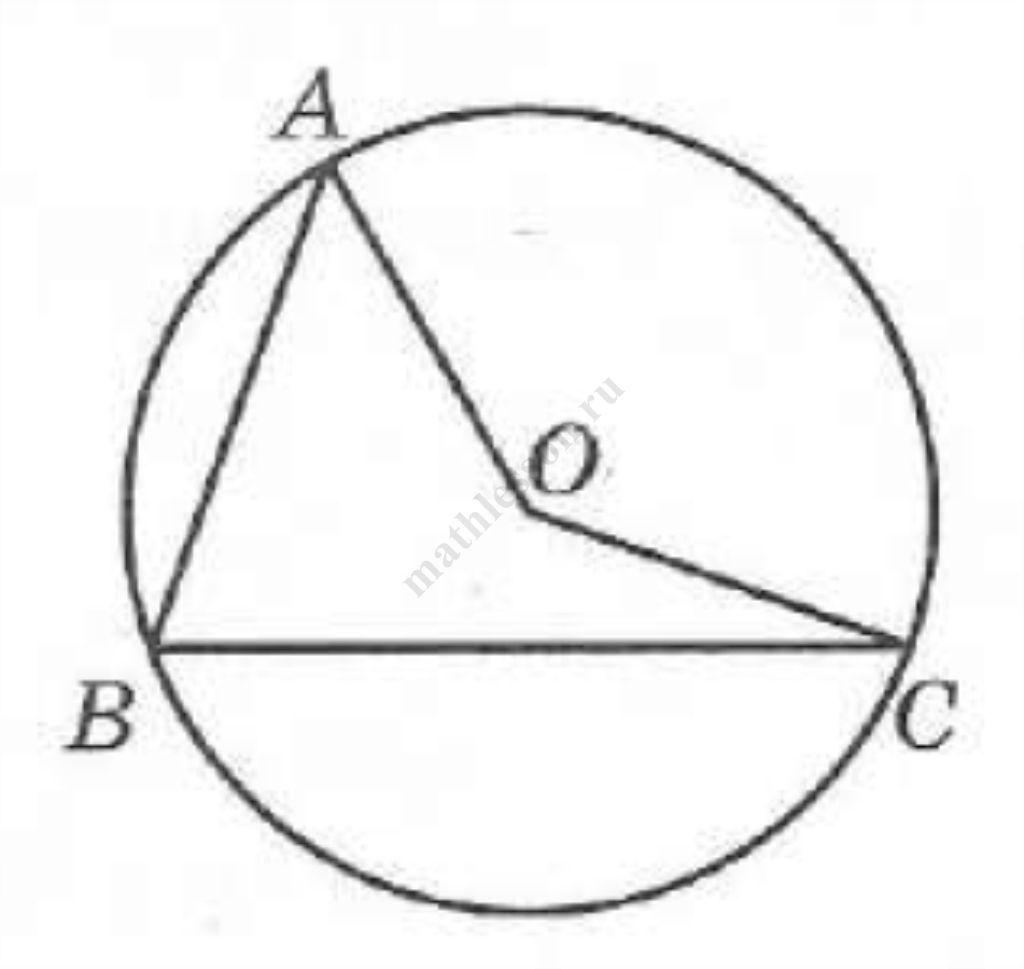
Задание 11
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Радиус окружности, описанной около треугольника, можно вычислить по формуле $$R = \frac{a}{2 \sin \alpha}$$, где $$a$$ — сторона, а $$\alpha$$ — противолежащий ей угол треугольника. Пользуясь этой формулой, найдите $$R$$, если $$a = 10$$ и $$\sin \alpha = \frac{1}{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$2x - 8 > 4x + 6$$
1) $$( -\infty;\ 1 )$$
2) $$( 1;\ +\infty )$$
3) $$( -\infty;\ -7 )$$
4) $$( -7;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


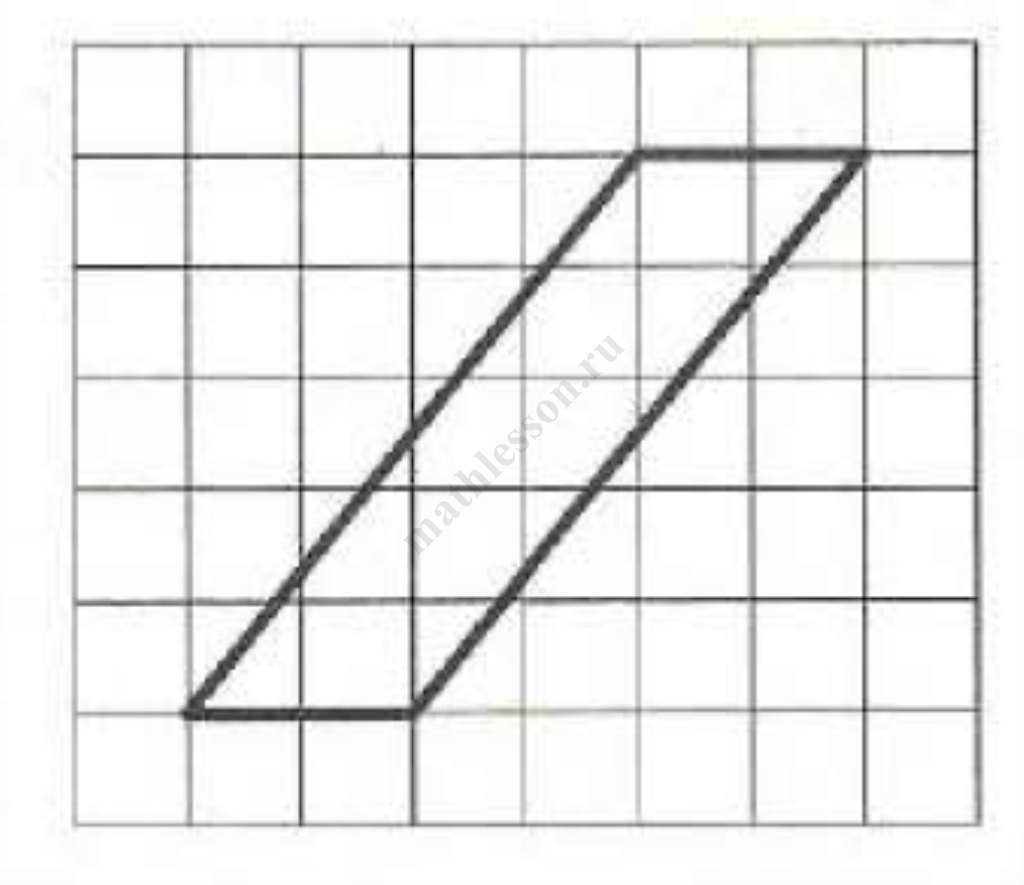
Задание 14
Каждое простейшее одноклеточное животное — инфузория-туфелька — размножается делением на $$2$$ части. Сколько инфузорий было первоначально, если после шестикратного деления их стало $$1280$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Катеты прямоугольного треугольника равны $$12$$ и $$5$$. Найдите гипотенузу этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


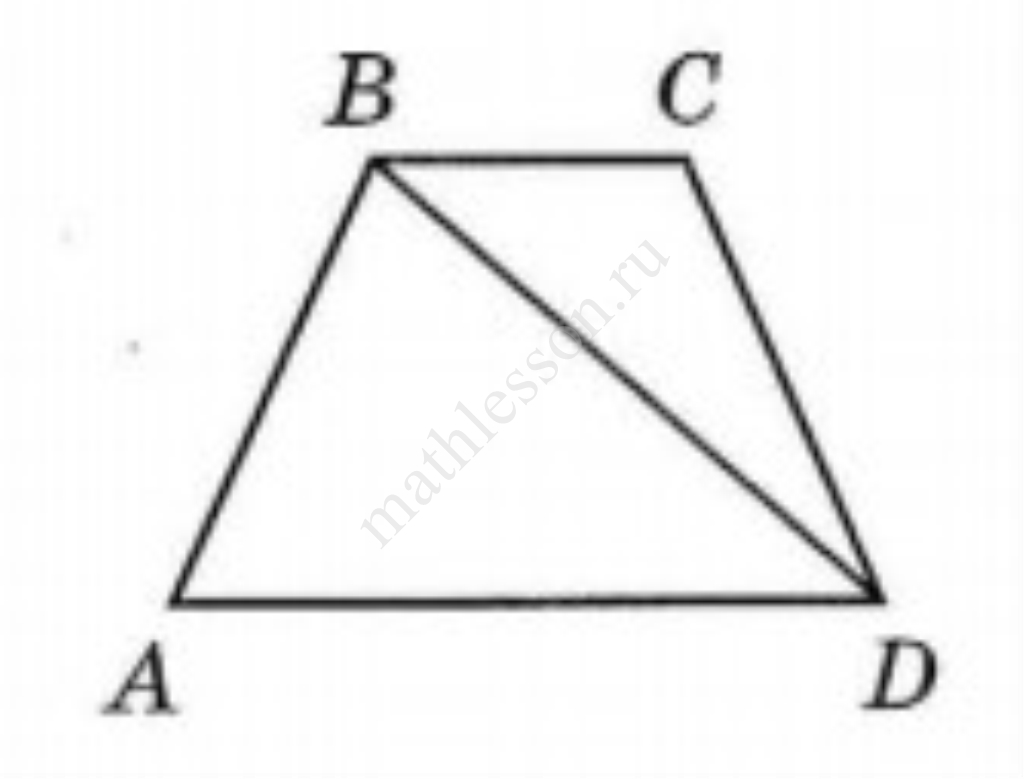
Задание 17
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
- Площадь трапеции равна произведению основания трапеции на высоту.
- Треугольника со сторонами $$1$$, $$2$$, $$4$$ не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Переносим всё в левую часть: $$x^3 + 7x^2 - 4x - 28 = 0.$$
2) Группируем: $$x^2(x+7) - 4(x+7) = 0.$$
3) Выносим общий множитель: $$(x+7)(x^2 - 4) = 0.$$
4) Разложение: $$x^2 - 4 = (x-2)(x+2),$$ поэтому $$(x+7)(x-2)(x+2) = 0.$$
5) Приравниваем множители к нулю: $$x+7=0,\quad x-2=0,\quad x+2=0.$$ Получаем: $$x = -7,\; 2,\; -2.$$
Задание 21
Грузовик перевозит партию щебня массой $$120$$ тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено $$3$$ тонны щебня. Определите, сколько тонн щебня было перевезено за последний день, если вся работа была выполнена за $$10$$ дней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \frac{|x| - 1}{|x| - x^2}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ не имеет с графиком общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Отрезки $$AB$$ и $$CD$$ являются хордами окружности. Найдите расстояние от центра окружности до хорды $$CD$$, если $$AB=20$$, $$CD=48$$, а расстояние от центра окружности до хорды $$AB$$ равно $$24$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Высоты $$BB_{1}$$ и $$CC_{1}$$ остроугольного треугольника $$ABC$$ пересекаются в точке $$E$$. Докажите, что углы $$CC_{1}B_{1}$$ и $$CBB_{1}$$равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
В выпуклом четырёхугольнике $$ABCD$$ диагонали пересекаются в точке $$O$$. Точка $$F$$ принадлежит отрезку $$AC$$. Известно, что $$BO=10$$, $$DO=14$$, $$AC=18$$. Найдите $$AF$$, если площадь треугольника $$FBC$$ в четыре раза меньше площади четырёхугольника $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!