ОГЭ 2022. Вариант 21 Ященко 36 вариантов ФИПИ школе.
Решаем 21 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 21 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
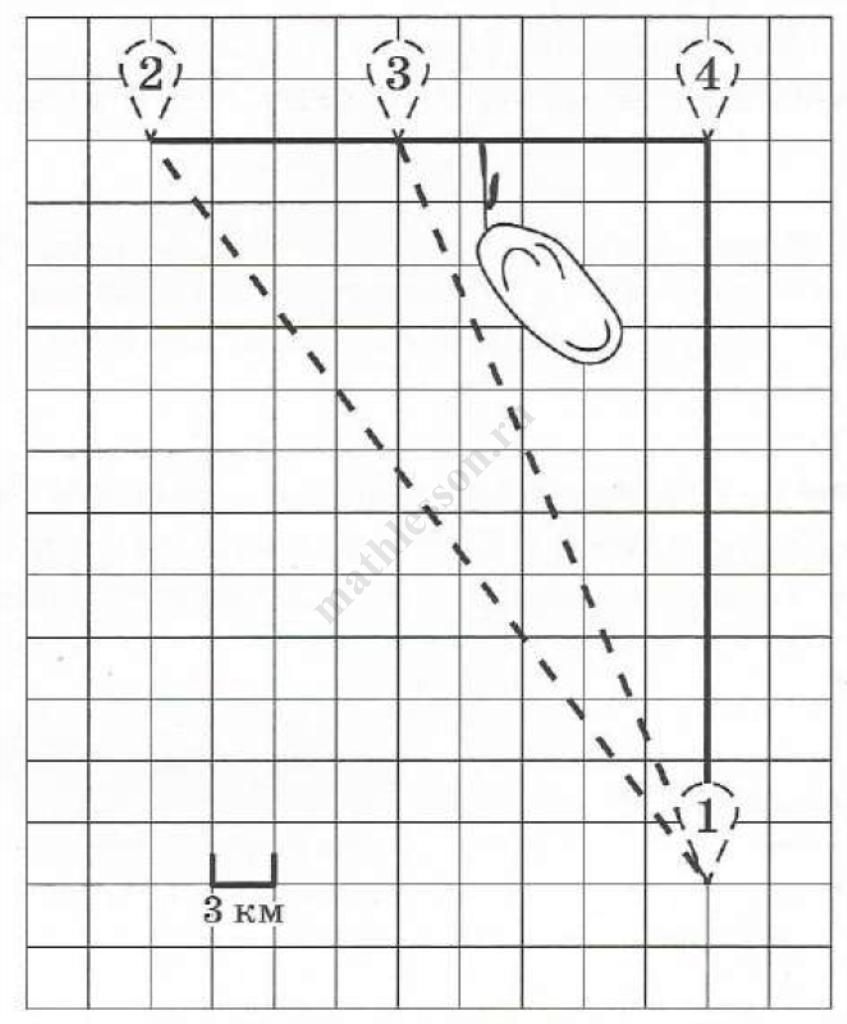
Дима летом отдыхает у дедушки в деревне Васильевке. Во вторник они собираются съездить на велосипедах в село Плодородное на ярмарку. Из деревни Васильевки в село Плодородное можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Шарковку до деревни Рассвет, где нужно повернуть под прямым углом направо па другое шоссе, ведущее в село Плодородное. Есть и третий маршрут: в деревне Шарковке можно свернуть па прямую тропинку в село Плодородное, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Дима с дедушкой едут со скоростью 25 км/ч, а по лесной дорожке и тропинке — со скоростью 18 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 3 км.
1) Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Насел. пункты | д. Васильевка | д. Шарковка | д. Рассвет |
| Цифры |
2) Сколько километров проедут Дима с дедушкой от деревни Васильевки до села Плодородного, если они поедут по шоссе через деревню Рассвет?
3) Найдите расстояние от деревни Шарковки до села Плодородного по прямой. Ответ дайте в километрах.
4) Сколько минут затратят на дорогу из деревни Васильевки в село Плодородное Дима с дедушкой, если они поедут сначала по шоссе, а затем свернут в Шарковке на прямую тропинку, которая проходит мимо пруда?
5) В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Васильевке, селе Плодородном, деревне Шарковке и деревне Рассвет.
| Наименование продукта | д. Васильевка | с. Плодородное | д. Шарковка | д. Рассвет |
| Молоко (1 л) | 37 | 38 | 36 | 39 |
| Хлеб (1 батон) | 16 | 18 | 22 | 21 |
| Сыр «Российский» (1 кг) | 240 | 280 | 250 | 260 |
| Говядина (1 кг) | 420 | 430 | 415 | 410 |
| Картофель (1 кг) | 30 | 28 | 35 | 25 |
Дима с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$a^{-13} \cdot (a^5)^3$$ при $$a = 7$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Найдите решение уравнения: $$2x^2 + 5x - 7 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в $$4$$ раза меньше, чем с зелёным. Найдите вероятность того, что случайно выбранный пакетик окажется с зелёным чаем.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Радиус окружности, описанной около треугольника, можно вычислить по формуле $$R = \frac{a}{2 \sin \alpha}$$, где $$a$$ — сторона, а $$\alpha$$ — противолежащий ей угол треугольника. Пользуясь этой формулой, найдите $$R$$, если $$a = 10$$ и $$\sin \alpha = \frac{1}{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$2x - 8 > 4x + 6$$
1) $$( -\infty;\ 1 )$$
2) $$( 1;\ +\infty )$$
3) $$( -\infty;\ -7 )$$
4) $$( -7;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Каждое простейшее одноклеточное животное — инфузория-туфелька — размножается делением на $$2$$ части. Сколько инфузорий было первоначально, если после шестикратного деления их стало $$1280$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Катеты прямоугольного треугольника равны $$12$$ и $$5$$. Найдите гипотенузу этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
- Площадь трапеции равна произведению основания трапеции на высоту.
- Треугольника со сторонами $$1$$, $$2$$, $$4$$ не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Переносим всё в левую часть: $$x^3 + 7x^2 - 4x - 28 = 0.$$
2) Группируем: $$x^2(x+7) - 4(x+7) = 0.$$
3) Выносим общий множитель: $$(x+7)(x^2 - 4) = 0.$$
4) Разложение: $$x^2 - 4 = (x-2)(x+2),$$ поэтому $$(x+7)(x-2)(x+2) = 0.$$
5) Приравниваем множители к нулю: $$x+7=0,\quad x-2=0,\quad x+2=0.$$ Получаем: $$x = -7,\; 2,\; -2.$$
Задание 21
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя $$20$$ минут, когда одному из них оставалось $$400$$ м до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг $$1$$ минуту назад. Найдите скорость (в км/ч) первого бегуна, если известно, что она на $$2$$ км/ч меньше скорости второго.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \left\{ \begin{aligned} x^2 + 2,&\ x \ge -2 \\ \frac{6}{-x},&\ x < -2 \end{aligned} \right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Отрезки $$AB$$ и $$CD$$ являются хордами окружности. Найдите расстояние от центра окружности до хорды $$CD$$, если $$AB=20$$, $$CD=48$$, а расстояние от центра окружности до хорды $$AB$$ равно $$24$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Высоты $$BB_{1}$$ и $$CC_{1}$$ остроугольного треугольника $$ABC$$ пересекаются в точке $$E$$. Докажите, что углы $$CC_{1}B_{1}$$ и $$CBB_{1}$$равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
В выпуклом четырёхугольнике $$ABCD$$ диагонали пересекаются в точке $$O$$. Точка $$F$$ принадлежит отрезку $$AC$$. Известно, что $$BO=10$$, $$DO=14$$, $$AC=18$$. Найдите $$AF$$, если площадь треугольника $$FBC$$ в четыре раза меньше площади четырёхугольника $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!