ОГЭ 2021. Вариант 36 Ященко 36 вариантов ФИПИ школе.
Решаем 36 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 36 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
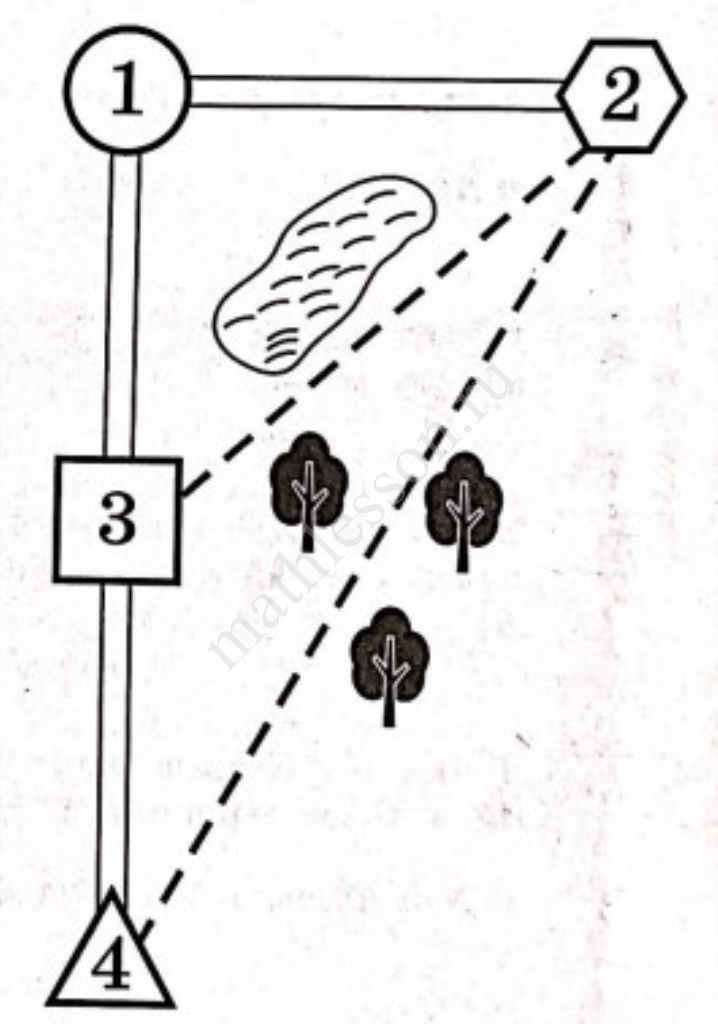
Настя летом отдыхает у дедушки и бабушки в селе Починки. Настя с дедушкой собираются съездить на машине на железнодорожную станцию Акулово. Из Починок в Акулово можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Вёшки до деревни Ухватово, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Акулово. Есть и третий маршрут: в Вёшках можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Акулово.
По шоссе Настя с дедушкой едут со скоростью 70 км/ч, а по грунтовым дорогам 48 км/ч. Расстояние по шоссе от Починок до Вёшек равно 28 км, от Починок до Ухватово — 64 км, а от Ухватово до Акулово — 48 км.
1) Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Нас. пункты | ст. Акулово | д. Вёшки | с. Починки | д. Ухватово |
| Цифры |
2) Сколько километров проедут Настя с дедушкой, если они поедут на станцию по шоссе через Ухватово?
3) Найдите расстояние от д. Вёшки до ст. Акулово по прямой. Ответ дайте в километрах.
4) Сколько минут затратят на дорогу Настя с дедушкой, если поедут на станцию по прямой грунтовой дороге от Починок до Акулово?
5) Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Маша с дедушкой, если поедут этим маршрутом.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$(\frac{11}{12}+\frac{11}{20})\cdot \frac{15}{8}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\frac{a^{18} \cdot (b^3)^5}{(ab)^{16}}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На олимпиаде по биологии участников рассаживали по трём аудиториям. В первых двух аудиториях посадили по $$130$$ человек, оставшихся проводили в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было $$400$$ участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние $$s$$ по формуле $$s = n \cdot l$$, где $$n$$ — число шагов, $$l$$ — длина шага. Какое расстояние прошёл человек, если $$l = 50$$ см, $$n = 1700$$? Ответ дайте в метрах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение системы неравенств:
$$\left\{\begin{aligned} 4 - 2x > -6 \\ 4x - 6 2 \end{aligned}\right.$$
1) $$( -\infty;\ 1 )$$
2) $$( 1;\ 2 )$$
3) $$( -\infty;\ 2 )$$
4) нет решений
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
К концу $$2012$$ года в городе проживало $$62\ 000$$ человек. Каждый год число жителей города возрастало на одну и ту же величину. В конце $$2019$$ года в городе проживало $$69\ 070$$ человек. Какова была численность населения этого города к концу $$2015$$ года?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
- Площадь параллелограмма равна половине произведения его диагоналей.
- Вписанный угол, опирающийся на диаметр окружности, прямой.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите систему уравнений: $$\left\{\begin{aligned} (x + 4)(y - 7) = 0 \\ \frac{x - 5}{x + y - 12} = 3 \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Из первого уравнения: $$(x+4)(y-7)=0 \Rightarrow x=-4$$ или $$y=7.$$
1) Пусть $$x=-4.$$ Тогда второе уравнение: $$\dfrac{-4-5}{-4+y-12}=3 \;\Rightarrow\; \dfrac{-9}{y-16}=3.$$ Отсюда $$-9=3(y-16) \;\Rightarrow\; y-16=-3 \;\Rightarrow\; y=13.$$ Знаменатель $$x+y-12=-4+13-12=-3\neq 0,$$ значит, пара $$(-4;13)$$ подходит.
2) Пусть $$y=7.$$ Тогда $$\dfrac{x-5}{x+7-12}=\dfrac{x-5}{x-5}=3.$$ Если $$x\neq 5,$$ левая часть равна $$1,$$ получаем противоречие $$1=3.$$ Если $$x=5,$$ знаменатель равен нулю. Следовательно, при $$y=7$$ решений нет.
Задание 21
Первый рабочий за час делает на $$9$$ деталей больше, чем второй, и выполняет заказ, состоящий из $$216$$ деталей, на $$4$$ часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \frac{1}{2} \left( \left| \frac{x}{3} - \frac{3}{x} \right| + \frac{x}{3} + \frac{3}{x} \right)$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Высота $$AH$$ ромба $$ABCD$$ делит сторону $$CD$$ на отрезки $$DH=15$$ и $$CH=2$$. Найдите высоту ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Точка $$K$$ — середина боковой стороны $$CD$$ трапеции $$ABCD$$. Докажите, что площадь треугольника $$KAB$$ равна половине площади трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
Точки $$M$$ и $$N$$ лежат на стороне $$AC$$ треугольника $$ABC$$ на расстояниях соответственно $$9$$ и $$32$$ от вершины $$A$$. Найдите радиус окружности, проходящей через точки $$M$$ и $$A$$ и касающейся луча $$AB$$, если $$\cos \angle BAC=\frac{2\sqrt{2}}{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!