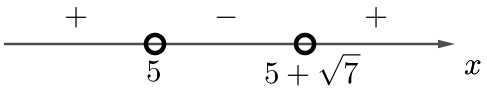ОГЭ 2021. Вариант 10 Ященко 36 вариантов ФИПИ школе.
Решаем 10 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 10 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Шины
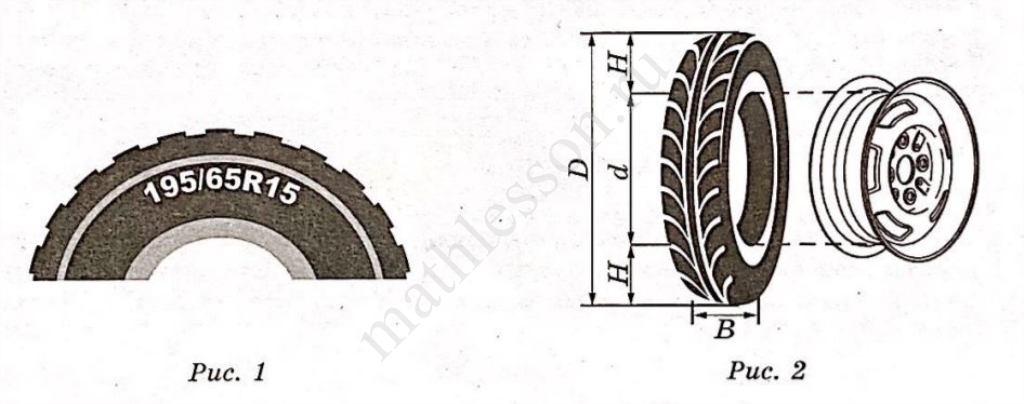
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины н (параметр Н на рисунке 2) к ширине шины, то есть $$100\cdot \frac{H}{B}$$
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие. Завод производит легковые автомобили определённой модели и устанавливает на них шины с маркировкой 185/60 R16.
1) Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Диаметр диска (дюймы)\Ширина шины (мм) | 14 | 15 | 16 | 17 |
| 175 | 175/70 | 175/65 | Не разр. | Не разр. |
| 185 | 185/70 | 185/60 | 185/55 | Не разр. |
| 195 | 195/65 | 195/60 | 195/50, 195/55 | 195/45 |
| 205 | 205/60 | 205/55 | 205/50 | 205/45 |
| 215 | Не разр. | Не разр. | 215/45 | 215/40 |
Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.
2) На сколько миллиметров радиус колеса с маркировкой 175/65 R15 больше, чем радиус колеса с маркировкой 205/55 R15?
3) Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
4) На сколько миллиметров увеличится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 205/45 R17?
5) На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 205/45 R17? Округлите результат до десятых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$15\cdot(\frac{3}{20}+\frac{7}{30})$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из данных чисел принадлежит промежутку $$[6; 7]$$?
1) $$\sqrt{6}$$
2) $$\sqrt{7}$$
3) $$\sqrt{38}$$
4) $$\sqrt{50}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\frac{6}{x+8}=-\frac{3}{4}\Leftrightarrow$$ $$6(-4)=(x+8)*3\Leftrightarrow$$ $$2(-4)=x+8\Leftrightarrow$$ $$-8-8=x\Leftrightarrow$$ $$x=-16$$
Задание 10
В фирме такси в данный момент свободно $$50$$ машин: $$15$$ чёрных, $$23$$ жёлтых и $$12$$ зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет зелёное такси.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Площадь треугольника вычисляется по формуле $$S = \frac{1}{2}bc \cdot \sin \alpha$$, где $$b$$ и $$c$$ — две стороны треугольника, а $$\alpha$$ — угол между ними. Пользуясь этой формулой, найдите величину $$\sin \alpha$$, если $$b = 10$$, $$c = 5$$ и $$S = 20$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Курс воздушных ванн начинают с $$15$$ минут в первый день и увеличивают время этой процедуры в каждый следующий день на $$5$$ минут. В какой по счёту день продолжительность процедуры достигнет $$1$$ часа?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
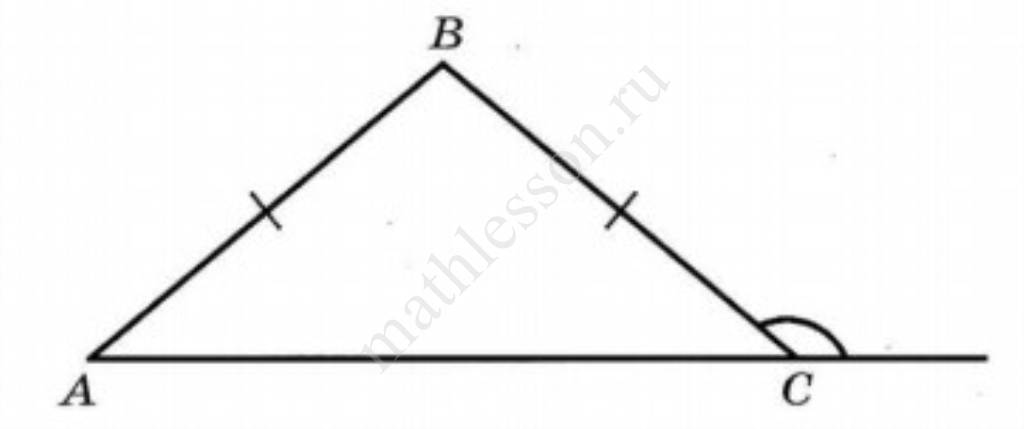
Сторона $$AC$$ треугольника $$ABC$$ проходит через центр описанной около него окружности. Найдите $$\angle C$$, если $$\angle A = 33^\circ$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Периметр ромба равен $$56$$, а один из углов равен $$30^\circ$$. Найдите площадь ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Площадь квадрата равна произведению двух его смежных сторон.
- Диагональ трапеции делит её на два равных треугольника.
- Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$(x - 5)^2 \sqrt{7}(x - 5)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Переносим всё в левую часть: $$(x - 5)^2 - \sqrt{7}(x - 5) < 0.$$ Выносим общий множитель: $$(x - 5)\bigl((x - 5) - \sqrt{7}\bigr) < 0.$$ То есть $$(x - 5)(x - 5 - \sqrt{7}) < 0.$$
2) Нули: $$x_1 = 5, x_2 = 5 + \sqrt{7}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 5)(x - 5 - \sqrt{7})$$ на полученных интервалах:
Выражение отрицателено при: $$x \in (5;\, 5 + \sqrt{7}).$$
Задание 21
Первая труба пропускает на $$15$$ литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом $$100$$ литров она заполняет на $$6$$ минут дольше, чем вторая труба?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \left\{ \begin{aligned} -x^2 - 2x + 3,&\ x \ge -2 \\ -x + 1,&\ x < -2 \end{aligned} \right.$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Известно, что около четырёхугольника $$ABCD$$ можно описать окружность и что продолжения сторон $$AB$$ и $$CD$$ четырёхугольника пересекаются в точке $$M$$. Докажите, что треугольники $$MBC$$ и $$MDA$$ подобны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
На стороне $$BC$$ остроугольного треугольника $$ABC$$ ($$AB\neq AC$$) как на диаметре построена полуокружность, пересекающая высоту $$AD$$ в точке $$M$$, $$AD=90$$, $$MD=69$$, $$H$$ - точка пересечения высот треугольника $$ABC$$. Найдите $$AH$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!