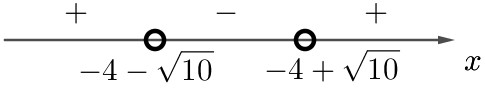ОГЭ 2021. Вариант 5. Ященко 36 вариантов ФИПИ школе.
Решаем 5 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 5 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
План местности
Миша летом отдыхает у дедушки и бабушки в деревне Николаевке. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе — через деревню Свистуху до деревни Берёзовки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево. Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево. По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Николаевки до Свистухи равно 16 км, от Николаевки до Берёзовки — 36 км, а от Берёзовки до Игнатьево 15 км.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Насел. пункты | д. Берёзовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры |
Задание 2.
Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
Задание 3.
Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
Задание 4.
Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
Задание 5.
Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минту потратят на дорогу Миша с дедушкой , если проедут этим маршрутом
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\sqrt{0,36p^4q^8}$$, при $$p = 5$$ и $$q = 2$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 + 8x + 15 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Закон Джоуля–Ленца можно записать в виде $$Q = I^2 R t$$, где $$Q$$ — количество теплоты (в джоулях), $$I$$ — сила тока (в амперах), $$R$$ — сопротивление цепи (в омах), а $$t$$ — время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи $$R$$ (в омах), если $$Q = 1296$$ Дж, $$I = 9$$ А, $$t = 2$$ с.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$(x + 2)(x - 10) > 0$$
1) $$( -2;\ 0 )$$
2) $$( -\infty;\ -2 ) \cup ( 10;\ +\infty )$$
3) $$( 10;\ +\infty )$$
4) $$( -2;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В амфитеатре $$20$$ рядов. В первом ряду $$56$$ мест, а в каждом следующем — на $$2$$ места меньше, чем в предыдущем. Сколько всего мест в амфитеатре?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Площадь параллелограмма можно найти по формуле $$S=a\cdot h$$, где $$a$$ - длина стороны параллелограмма, $$h$$ - длина высоты, проведенной к этой стороне.
$$S=(3+5)\cdot 12=96$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$\frac{-18}{(x+4)^2 - 10} \ge 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Числитель $$-18$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была положительной, знаменатель должен быть отрицательным: $$(x+4)^2 - 10 < 0.$$
2) Решим неравенство: $$(x+4)^2 - 10 < 0.$$ Учтём, что $$(x+4)^2 - 10 = (x + 4)^2 - (\sqrt{10})^2 = (x+4-\sqrt{10})(x+4+\sqrt{10}).$$ Нули $$x_1 = -4 - \sqrt{10};\quad x_2 = -4 + \sqrt{10}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x+4-\sqrt{10})(x+4+\sqrt{10})$$ на полученных промежутках:
Выражение отрицательное при: $$x \in (-4-\sqrt{10};\,-4+\sqrt{10}).$$
Задание 21
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на $$51$$ минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет $$251$$ км, скорость первого велосипедиста равна $$10$$ км/ч, скорость второго — $$20$$ км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \frac{(x + 3)(x^2 - 3x + 2)}{x - 2}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
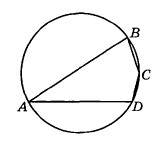
Окружность пересекает стороны $$AB$$ и $$AC$$ треугольника $$ABC$$ в точках $$K$$ и $$P$$ соответственно и проходит через вершины $$B$$ и $$C$$. Найдите длину отрезка $$KP$$, если $$AP=34$$, а сторона $$BC$$ в $$2$$ раза меньше стороны $$AB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!