ОГЭ 2023. Вариант 12 Ященко 36 вариантов ФИПИ школе.
Решаем 12 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 12 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Печи
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 2,8 м, ширина 2,5 м, высота 2,2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 5800 руб.
| Номер печи | Тип | Объём помещения (куб. м) | Масса (кг) | Стоимость (руб.) |
| 1 | дровяная | 9-14 | 40 | 17 500 |
| 2 | дровяная | 11-16,5 | 48 | 19 000 |
| 3 | электрическая | 10-16 | 15 | 13 500 |
1. Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Объём (куб. м) | 9 | 10 | 11 |
| Номер печи |
2. Найдите объём парного отделения строящейся бани. Ответ дайте в кубических метрах.
3. Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 1800 рублей?
4. На дровяную печь, масса которой 40 кг, сделали скидку 10 %. Сколько рублей стала стоить печь?
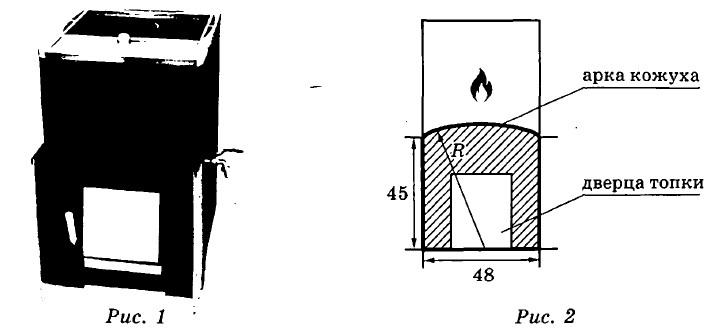
5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки $$R$$. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Задание 6
Найдите значение выражения $$(1\frac{11}{16}-3\frac{7}{8})\cdot 4$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из данных ниже чисел принадлежит отрезку $$[3; 4]$$?
1) $$\frac{47}{14}$$
2) $$\frac{57}{14}$$
3) $$\frac{61}{14}$$
4) $$\frac{65}{14}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 - 144 = 0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Задание 10
В среднем из $$150$$ карманных фонариков, поступивших в продажу, $$6$$ — неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Энергия заряженного конденсатора $$W$$ (в Дж) вычисляется по формуле $$W = \frac{CU^2}{2}$$, где $$C$$ — ёмкость конденсатора (в Ф), а $$U$$ — разность потенциалов на обкладках конденсатора (в В). Найдите энергию конденсатора (в Дж) ёмкостью $$10^{-4}$$ Ф, если разность потенциалов на обкладках конденсатора равна $$22$$ В.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение системы неравенств:
$$\left\{\begin{aligned} -48 + 6x > 0 \\ 6 - 5x > -4 \end{aligned}\right.$$
1) $$( 2;\ 8 )$$
2) $$( -\infty;\ 2 )$$
3) нет решений
4) $$( 8;\ +\infty )$$
Задание 14
В амфитеатре $$15$$ рядов. В первом ряду $$20$$ мест, а в каждом следующем — на $$2$$ места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
Задание 15
Прямая, параллельная стороне $$AC$$ треугольника $$ABC$$, пересекает стороны $$AB$$ и $$BC$$ в точках $$M$$ и $$N$$ соответственно, $$AC = 36$$, $$MN = 28$$. Площадь треугольника $$ABC$$ равна $$162$$. Найдите площадь треугольника $$MBN$$.
Задание 19
Какое из следующих утверждений верно?
- Сумма углов выпуклого четырёхугольника равна $$360^{\circ}$$.
- Средняя линия трапеции равна сумме её оснований.
- Любой параллелограмм можно вписать в окружность.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите уравнение $$ x^2 - 3x + \sqrt{5 - x} = \sqrt{5 - x} + 18 $$
1) ОДЗ: $$5 - x \ge 0 \;\Rightarrow\; x \le 5.$$
2) Уберём одинаковый корень по обе стороны: $$x^2 - 3x = 18,$$ $$x^2 - 3x - 18 = 0.$$
3) Решим квадратное уравнение: $$D = (-3)^2 - 4\cdot 1\cdot(-18) = 9 + 72 = 81,$$ $$x_{1,2} = \dfrac{3 \pm \sqrt{81}}{2} = \dfrac{3 \pm 9}{2}.$$ Получаем $$x_1 = 6,\quad x_2 = -3.$$ С учётом $$x \le 5$$ подходит только $$x = -3.$$
Задание 21
Теплоход проходит по течению реки до пункта назначения $$80$$ км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна $$5$$ км/ч, стоянка длится $$23$$ часа, а в пункт отправления теплоход возвращается через $$35$$ часов после отплытия из него.
Задание 22
Постройте график функции $$y = x^2 - |4x + 7|$$. Определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Задание 23
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Найдите длину отрезка $$EF$$, если $$AD=48$$, $$BC=16$$, $$CF:DF=5:3$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Через точку $$O$$ пересечения диагоналей параллелограмма $$ABCD$$ проведена прямая, пересекающая стороны $$AB$$ и $$CD$$ в точках $$P$$ и $$Q$$ соответственно. Докажите, что отрезки $$BP$$ и $$DQ$$ равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=4:9$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$AKM$$ к площади треугольника $$KPCM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Пусть $$S_{ABC}=S\to S_{ABM}=S_{BMC}=\frac{S}{2}.$$
2) $$\frac{S_{ABK}}{S_{AKM}}=\frac{BK}{KM}=\frac{4}{9}\to S_{AKM}=\frac{9}{13}S_{ABM}\frac{9}{13}\cdot \frac{S}{2}=\frac{9S}{26}.$$
3) Пусть $$ML\parallel AP\to ML$$ - средняя линия $$\triangle APL$$ и $$PL=LC.$$ Но $$KP\parallel ML\to \frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{9},$$ тогда $$\frac{BP}{PC}=\frac{4}{18}.$$
4) $$\frac{S_{APC}}{S_{ABC}}=\frac{PC}{BC}=\frac{18}{22}\to S_{APC}=\frac{9}{11}S\to S_{KPOM}=S_{APC}-S_{AKM}=\frac{9S}{11}-\frac{9S}{26}=$$ $$=\frac{9S(26-11)}{26\cdot 11}=\frac{15\cdot 9S}{26\cdot 11}\to \frac{S_{AKM}}{S_{KPCM}}=\frac{9}{26}\cdot \frac{26\cdot 11}{15\cdot 9}=\frac{11}{15}.$$