Задание 125
Задание 125
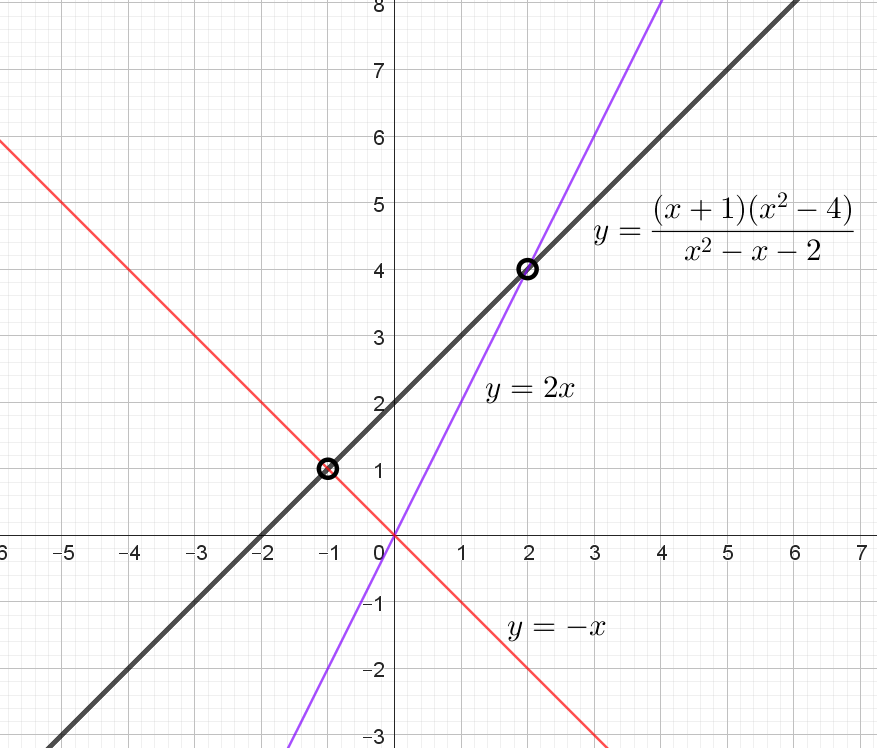
Постройте график функции $$y = \frac{(x+1)(x^2-4)}{x^2-x-2}$$
Определите, при каких значениях $$k$$ прямая $$y=kx$$ не имеет с графиком общих точек.
Разложим знаменатель на множители: $$x^2 - x - 2 = (x - 2)(x + 1)$$. Учтем, что $$x^2 - 4 = (x - 2)( x+ 2)$$
$$y = \frac{(x+1)(x-2)(x+2)}{(x-2)(x+1)} = x + 2$$ при $$x \neq -1; 2$$, так как знаменатель не может равнять нулю.
То есть графиком функции будет прямая $$y = x + 2$$, с учетом, что $$x \neq -1; y \neq -1+2 =1$$ и $$x \neq 2; y \neq 2 + 2 = 4$$
Пустые точки на графике: $$(-1; 1)$$, $$(2; 4)$$. На рисунке итоговая прямая выделена черным цветом.
Прямая $$y = kx$$ не имеет общих точек при:
Проходит через $$(-1; 1)$$ - выделена красным цветом. Подставим координаты данной точки в уравнение прямой: $$1 = k \cdot (-1) \Leftrightarrow k = -1$$
Проходит через $$(2; 4)$$ - выделена синим цветом. Подставим координаты данной точки в уравнение прямой: $$4 = k \cdot 2 \Leftrightarrow k = 2$$
Задание 104
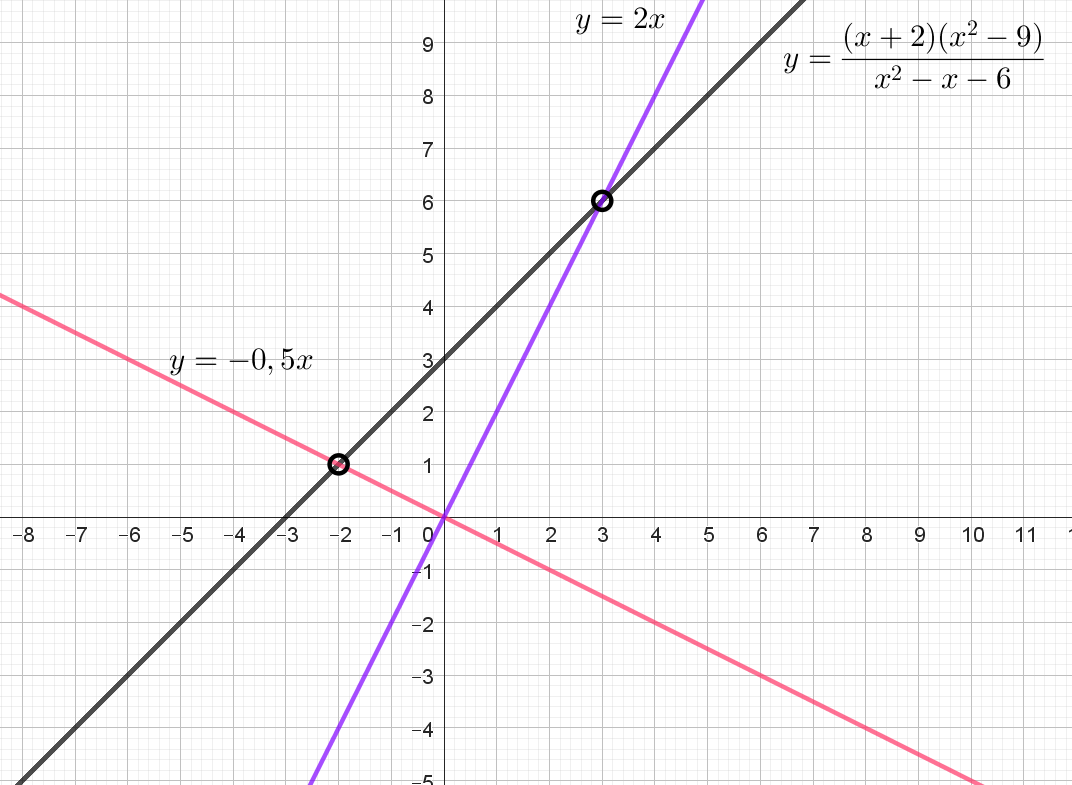
Постройте график функции $$y = \frac{(x+2)(x^2-9)}{x^2-x-6}$$
Определите, при каких значениях $$k$$ прямая $$y=kx$$ не имеет с графиком общих точек.
Разложим знаменатель на множители: $$x^2 - x - 6 = (x - 3)(x + 2)$$. Учтем, что $$x^2 - 9 = (x - 3)( x+ 3)$$
$$y = \frac{(x+2)(x-3)(x+3)}{(x-3)(x+2)} = x + 3$$ при $$x \neq -2; 3$$, так как знаменатель не может равнять нулю.
То есть графиком функции будет прямая $$y = x + 3$$, с учетом, что $$x \neq -2; y \neq -2+3 =1$$ и $$x \neq 3; y \neq 3 + 3 = 6$$
Пустые точки на графике: $$(-2; 1)$$, $$(3; 6)$$. На рисунке итоговая прямая выделена черным цветом.
Прямая $$y = kx$$ не имеет общих точек при:
Проходит через $$(-2; 1)$$ - выделена красным цветом. Подставим координаты данной точки в уравнение прямой: $$1 = k \cdot (-2) \Leftrightarrow k = -0,5$$
Проходит через $$(3; 6)$$ - выделена синим цветом. Подставим координаты данной точки в уравнение прямой: $$6 = k \cdot 3 \Leftrightarrow k = 2$$