ОГЭ 2024. Вариант 12 Ященко 36 вариантов ФИПИ школе.
Решаем 12 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 12 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Теплицы
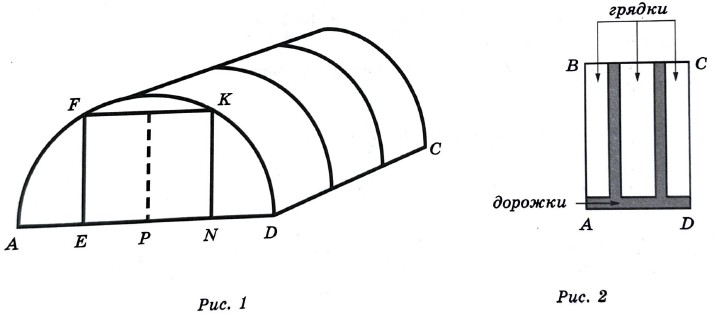
Глеб Сергеевич начал строить на дачном участке теплицу длиной 5 метров ( $$DC$$ на рис. 1). Для этого он сделал прямоугольный фундамент (рис. 2). Для каркаса теплицы нужно заказать металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки теплицы. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником $$EFKN$$, где точки $$E, P$$ и $$N$$ делят отрезок $$AD$$ на равные части.
Внутри теплицы Глеб Сергеевич планирует сделать три грядки, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером $$20 \times 20$$ см.
- Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
- Найдите ширину теплицы в метрах с точностью до десятых.
- Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 8 штук.
- Найдите площадь участка внутри теплицы, отведённого под грядки, в квадратных метрах. Результат округлите до десятых.
- Найдите высоту $$EF$$ входа в теплицу в сантиметрах с точностью до целого.
Задание 7
Какому из данных промежутков принадлежит число $$\frac{7}{11}$$?
1) $$[0,4; 0,5]$$
2) $$[0,5; 0,6]$$
3) $$[0,6; 0,7]$$
4) $$[0,7; 0,8]$$
Задание 8
Найдите значение выражения $$\sqrt{10 \cdot 7^2} \cdot \sqrt{10 \cdot 2^6}$$.
Задание 10
У бабушки $$20$$ чашек: $$11$$ с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Площадь четырёхугольника можно вычислить по формуле $$S = \frac{d_1 d_2 \sin \alpha}{2}$$, где $$d_1$$ и $$d_2$$ — длины диагоналей четырёхугольника, $$\alpha$$ — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали $$d_2$$, если $$d_1 = 9$$, $$\sin \alpha = \frac{5}{8}$$, $$S = 56,25$$.
Задание 14
В амфитеатре $$14$$ ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду $$27$$ мест, а в восьмом ряду $$36$$ место. Сколько мест в последнем ряду амфитеатра?
Задание 17
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите уравнение: $$(x + 2)^4 + (x + 2)^2 - 12 = 0$$
1) Замена: $$(x + 2)^2 = t.$$ Получаем $$t^2 + t - 12 = 0.$$
2) Дискриминант: $$D = 1^2 - 4\cdot 1\cdot(-12) = 1 + 48 = 49,$$ $$t_{1,2} = \dfrac{-1 \pm \sqrt{49}}{2} = \dfrac{-1 \pm 7}{2}.$$ Тогда $$t_1 = 3,\quad t_2 = -4.$$ Так как $$t = (x + 2)^2 \ge 0,$$ берём $$t = 3.$$
3) Возвращаемся к $$x$$: $$(x + 2)^2 = 3,$$ $$x + 2 = \pm \sqrt{3},$$ $$x = -2 \pm \sqrt{3}.$$
Задание 21
Первый велосипедист выехал из посёлка по шоссе со скоростью $$24$$ км/ч. Через час после него со скоростью $$21$$ км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через $$9$$ часа после этого догнал первого.
Задание 25
В треугольнике $$ABC$$ известны длины сторон $$AB=12$$, $$AC=72$$, точка $$O$$ - центр окружности, описанной около треугольника $$ABC$$. Прямая $$BD$$, перпендикулярная прямой $$AO$$, пересекает сторону $$AC$$ в точке $$D$$. Найдите $$CD$$.