ОГЭ 2021. Вариант 24 Ященко 36 вариантов ФИПИ школе.
Решаем 24 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 24 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Квартиры
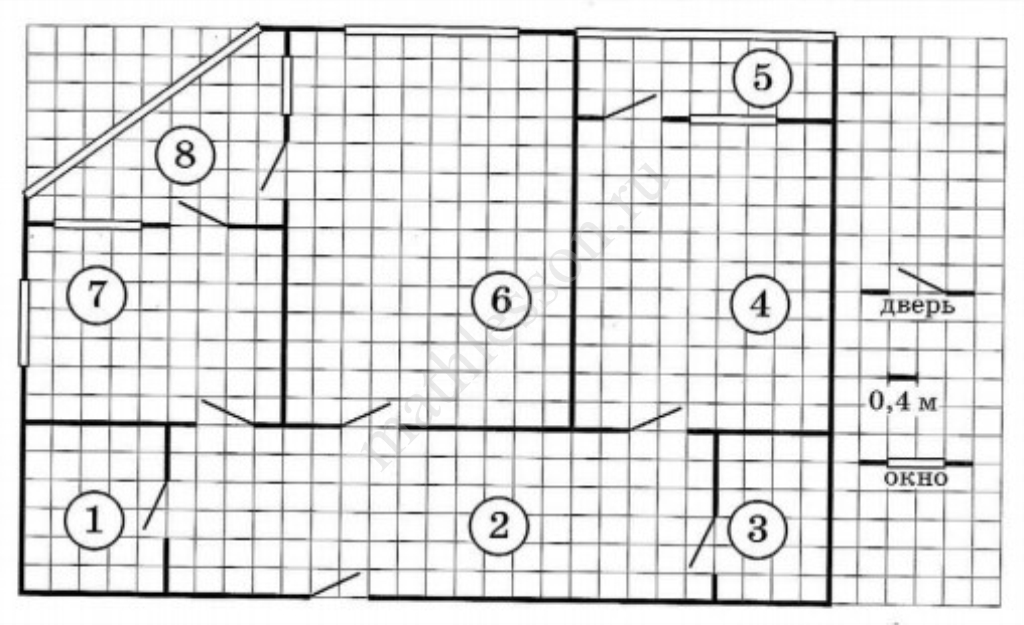
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Кроме неё в квартире есть ещё два помещения без окон — это санузел и кладовая, причём площадь кладовой меньше площади санузла. В квартире имеются две застеклённые лоджии. Одна из них — прямоугольной формы — примыкает к спальне. Другая — угловая. В кухне располагаются два одинаковых по ширине окна: одно выходит на улицу, а другое — на лоджию. В гостиной тоже два окна, но они разной ширины: узкое выходит на лоджию, а широкое — на улицу.
1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
| Помещения | гостиная | прихожая | спальня | кухня | санузел |
| Цифры |
2. Найдите ширину большего окна гостиной. Ответ дайте в сантиметрах.
3. Плитка для пола размером 30 см х 30 см продаётся в упаковках по 10 штук. Сколько упаковок плитки необходимо купить, чтобы выложить пол лоджии, примыкающей к спальне?
4. Найдите площадь угловой лоджии. Ответ дайте в квадратных метрах.
5. Сколько процентов составляет площадь гостиной от площади всей квартиры? Округлите ответ до десятых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Между какими числами заключено число $$\sqrt{73}$$?
1) $$8$$ и $$9$$
2) $$72$$ и $$74$$
3) $$24$$ и $$26$$
4) $$4$$ и $$5$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$2^9 \cdot \frac{2^{-2}}{2^2}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$7x^2 - 14x = 0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Длина биссектрисы $$l_c$$, проведённой к стороне $$c$$ треугольника со сторонами $$a$$, $$b$$ и $$c$$, вычисляется по формуле $$l_c = \frac{1}{a + b} \sqrt{ab\left((a + b)^2 - c^2\right)}$$. Найдите биссектрису $$l_c$$, если $$a = 4$$, $$b = 8$$, $$c = 6\sqrt{2}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
При каких значениях $$a$$ выражение $$6a + 7$$ принимает только отрицательные значения?
1) $$a > -\frac{6}{7}$$
2) $$a > -\frac{7}{6}$$
3) $$a -\frac{7}{6}$$
4) $$a -\frac{6}{7}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В амфитеатре $$16$$ рядов. В первом ряду $$54$$ места, а в каждом следующем — на $$2$$ места меньше, чем в предыдущем. Сколько всего мест в амфитеатре?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Сторона равностороннего треугольника равна $$16\sqrt{3}$$. Найдите его высоту.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Центр окружности, описанной около треугольника $$ABC$$, лежит на стороне $$AB$$. Радиус окружности равен $$10$$. Найдите $$BC$$, если $$AC = 16$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Найдите больший угол равнобедренной трапеции $$ABCD$$, если диагональ $$AC$$ образует с основанием $$AD$$ и боковой стороной $$AB$$ углы, равные $$36^\circ$$ и $$53^\circ$$ соответственно.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- В прямоугольном треугольнике гипотенуза равна сумме катетов.
- Всегда один из двух смежных углов острый, а другой тупой.
- Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Сумма квадратов равна нулю, значит $$ \begin{cases} x^2 - 49 = 0,\\ x^2 + 4x - 21 = 0. \end{cases} $$
2) Уравнение $$x^2 - 49 = 0.$$ Дискриминант: $$D = 0^2 - 4\cdot 1\cdot(-49) = 196,$$ $$x_{1,2} = \dfrac{0 \pm \sqrt{196}}{2} = \pm 7.$$ То есть $$x = 7,\ x = -7.$$
3) Уравнение $$x^2 + 4x - 21 = 0.$$ Дискриминант: $$D = 4^2 - 4\cdot 1\cdot(-21) = 16 + 84 = 100,$$ $$x_{1,2} = \dfrac{-4 \pm \sqrt{100}}{2} = \dfrac{-4 \pm 10}{2}.$$ Тогда $$x_1 = 3,\quad x_2 = -7.$$
4) Общий корень двух уравнений: $$x = -7.$$
Задание 21
Свежие фрукты содержат $$84 \%$$ воды, а высушенные — $$16 \%$$. Сколько килограммов сухих фруктов получится из $$231$$ кг свежих фруктов
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Биссектрисы углов $$B$$ и $$C$$ параллелограмма $$ABCD$$ пересекаются в точке $$T$$, лежащей на стороне $$AD$$. Докажите, что $$T$$ — середина $$AD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!