ОГЭ 2023. Вариант 22 Ященко 36 вариантов ФИПИ школе.
Решаем 22 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 22 варианта (всех заданий) Ященко 2023 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Квартиры
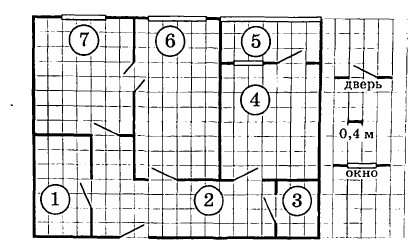
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Слева от входа в квартиру располагаются кухня и санузел, причём площадь кухни больше площади санузла. Наименьшую площадь имеет кладовая. Из гостиной есть двери в коридор и на кухню. В квартире есть застеклённая лоджия, куда можно попасть, пройдя через спальню.
1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
| Помещения | кухня | гостиная | кладовая | прихожая | спальня |
| Цифры |
2. Плитка для пола размером $$20 \times 10$$ см продаётся в упаковках по $$10$$ штук. Сколько упаковок плитки необходимо купить, чтобы выложить пол лоджии?
3. Найдите площадь кухни. Ответ дайте в квадратных метрах.
4. Сколько процентов составляет площадь гостиной от площади всей квартиры?
5. В квартире планируется заменить электрическую плиту. Характеристики электроплит, условия подключения и доставки приведены в таблице. Планируется купить электрическую плиту шириной $$50 \mathrm{~см}$$ с духовкой объёмом не менее 52 л.
| Модель | Объём духовки (л) | Максимальная температура ($$^\circ$$) | Стоимость плиты (руб.) | Стоимость подключения (руб.) | Стоимость доставки ($$\%$$ от стоимость плиты) | Габариты (высота*ширина*глубина, см) |
| А | 50 | 280 | 8890 | 1700 | бесплатно | $$85 \times 50 \times 54$$ |
| Б | 50 | 300 | 9790 | 750 | 10 | $$85 \times 50 \times 54$$ |
| В | 50 | 250 | 11690 | 700 | 10 | $$85 \times 60 \times 60$$ |
| Г | 52 | 250 | 17490 | 800 | 10 | $$85 \times 60 \times 60$$ |
| Д | 70 | 275 | 17990 | 1400 | бесплатно | $$85 \times 60 \times 45$$ |
| Е | 58 | 250 | 18890 | 1500 | бесплатно | $$85 \times 50 \times 60$$ |
| Ж | 54 | 270 | 18900 | 750 | 15 | $$85 \times 50 \times 60$$ |
| 3 | 46 | 250 | 20990 | 750 | 10 | $$87 \times 50 \times 60$$ |
| И | 70 | 275 | 21690 | 1500 | бесплатно | $$85 \times 50 \times 60$$ |
| К | 67 | 250 | 22990 | 1500 | бесплатно | $$85 \times 50 \times 60$$ |
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\frac{(b^{-5})^2}{b^{-12}}$$ при $$b = 5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$(x+2)^2=(1-x)^2$$ из этого получаем 2 уравнения:
1) $$x+2=1-x\to 2x=-1\to x=-0,5$$
2) $$x+2=x-1\to$$ корней нет
Задание 10
В магазине канцтоваров продаётся $$120$$ ручек: $$32$$ — красные, $$32$$ — зелёные, $$46$$ — фиолетовые, остальные — синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


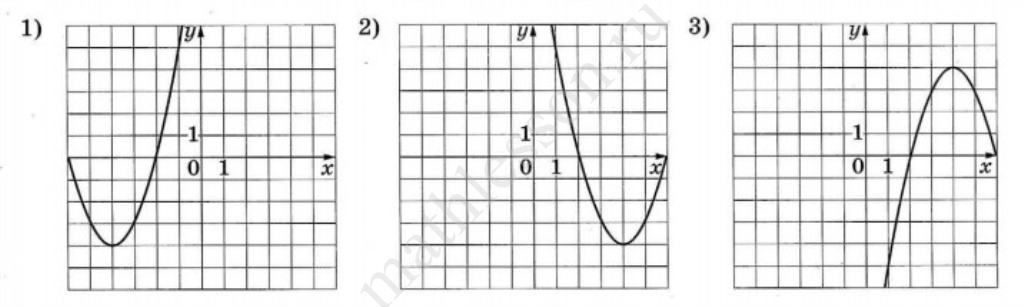
У 3-го ветви направлены вниз, значит $$a<0 (y=ax^2+bx+c)\to B.$$
Найдем абсциссу вершины для A: $$x_0=-\frac{8}{2}=-4\to$$ 1 график. Тогда 123.
Задание 12
Центростремительное ускорение при движении по окружности (в м/с²) вычисляется по формуле $$a = \omega^2 R$$, где $$\omega$$ — угловая скорость (в с⁻¹), $$R$$ — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус $$R$$, если угловая скорость равна $$7,5$$ с⁻¹, а центростремительное ускорение равно $$337,5$$ м/с². Ответ дайте в метрах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В течение $$20$$ банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в $$9$$-й день акция стоила $$555$$ рублей, а в $$13$$-й день — $$631$$ рубль?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Сторона треугольника равна $$16$$, а высота, проведённая к этой стороне, равна $$27$$. Найдите площадь этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Диагональ прямоугольника образует угол $$63^\circ$$ с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Касательная к окружности параллельна радиусу, проведённому в точку касания.
- Если в ромбе один из углов равен $$90^{\circ}$$ градусам, то этот ромб является квадратом.
- Сумма углов равнобедренного треугольника равна $$180^{\circ}$$ градусам.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) нет, перпендикулярна
2) да
3) да (любого треугольника)
Задание 20
Решите уравнение: $$x^6 = -(7x + 10)^3$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$x^6=-(7x+10)^3\leftrightarrow x^2=-(7x-10)\leftrightarrow x^2+7x+10=0.$$ Из этого получаем два уравнения:
1) $$x_1+x_2=-7\to x_1=-2$$
2) $$x_1\cdot x_2=10\to x_2=-5$$
Задание 21
Два велосипедиста одновременно отправились в $$224$$ - километровый пробег. Первый ехал со скоростью, на $$2$$ км/ч большей, чем скорость второго, и прибыл к финишу на $$2$$ час раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Пусть x км/ч - скорость второго, тогда $$x+2$$ км/ч - скорость первого. Получим: $$\frac{224}{x}-\frac{222}{x+2}=2\leftrightarrow 112(x+2)-112x=1(x^2+2x)\leftrightarrow$$ $$\leftrightarrow 112x+224-112x=x^2+2x\leftrightarrow x^2+2x-224=0$$
Решаем по теореме Виета:
1) $$x_1+x_2=-2\to x_1=-16<0$$
2) $$x_1x_2=-224\to x_2=14$$ - ответ.
Задание 22
Постройте график функции $$y = x^2 - 3|x| - x$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком не менее одной, но не более трёх общих точек.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$y=x^2-3|x|-x$$ получаем уравнения:
1) $$y=x^2-3x-x, x\geq 0 \to y=x^2-4x, x\geq 0 (1)$$
2) $$y=x^2+3x-x, x<0 \to y=x^2+2x, x<0 (2)$$
(1) $$x_0=-\frac{-4}{2}=2; y_0=2^2-4\cdot 2=-4.$$ Нули функции: $$x^2-4x=0\to x_1=0; x_2=4.$$
(2) $$x_0=-\frac{2}{2}=-1; y_0=(-1)^2+2(-1)=-1.$$ Нули функции: $$x^2+2x=0\to x_1=0; x_2=-2.$$
Построим график функции: $$y=m$$ - прямая, параллельная Ox от одной до трех точек пересечения имеет при $$m\in[-4;-1]\cup[0;+\infty)$$
Задание 23
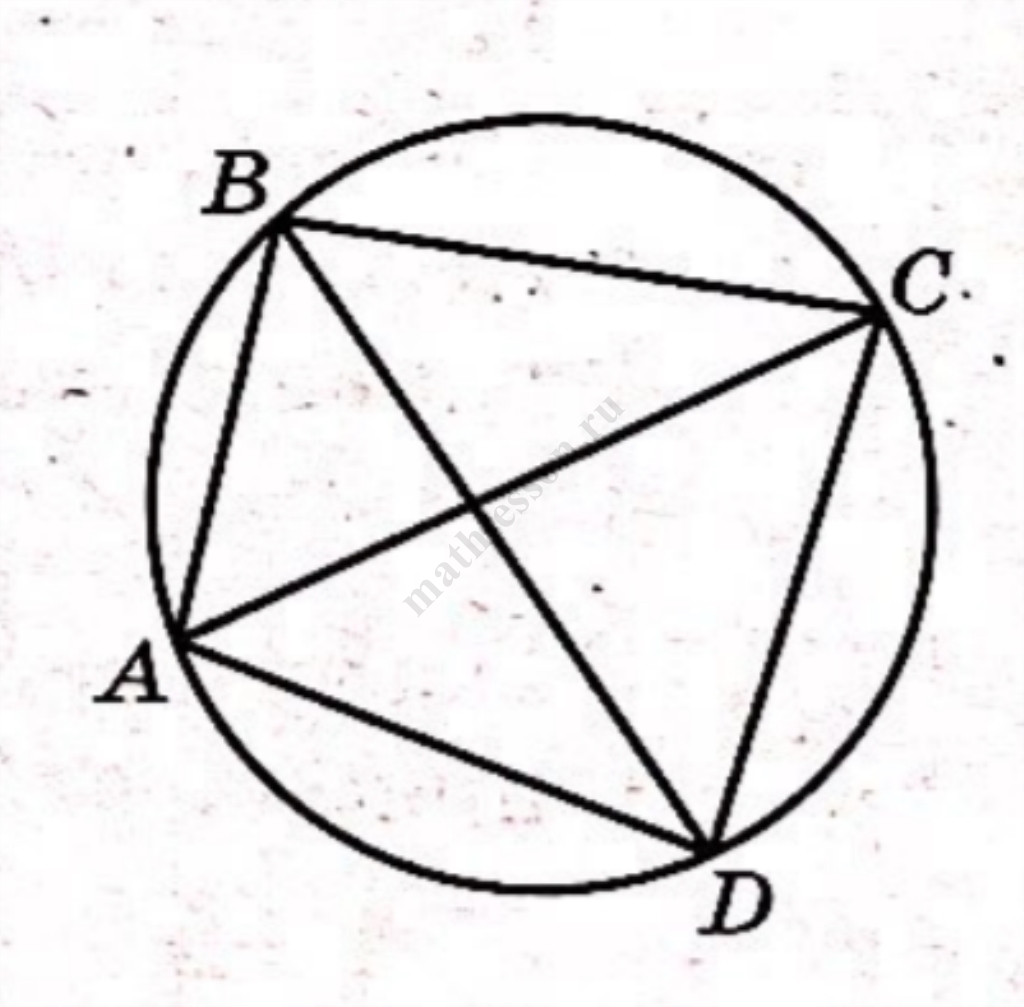
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как $$6:11:19$$. Найдите радиус окружности, если меньшая из сторон равна $$15$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Углы A,B,C - вписанные, потому равны половинам соответствующих дуг, потому отношение углов 6:11:29.
2) Т.к. $$\angle A+\angle B+\angle C=180^{\circ},$$ если $$\angle A=6x,$$ то: $$6x+11x+29x=180^{\circ}\to x=5\to \angle A=30^{\circ}.$$
3) Напротив меньшей стороны лежит меньший угол $$\to BC=15. R=\frac{a}{2\sin{\alpha}}=\frac{BC}{2\sin{A}}=\frac{15}{2\cdot \frac{1}{2}}=15$$
Задание 25
Биссектрисы углов $$A$$ и $$B$$ параллелограмма $$ABCD$$ пересекаются в точке $$K$$. Найдите площадь параллелограмма, если $$BC=2$$, а расстояние от точки $$K$$ до стороны $$AB$$ равно $$8$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!