ОГЭ 2021. Вариант 34 Ященко 36 вариантов ФИПИ школе.
Решаем 34 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 34 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Квартиры
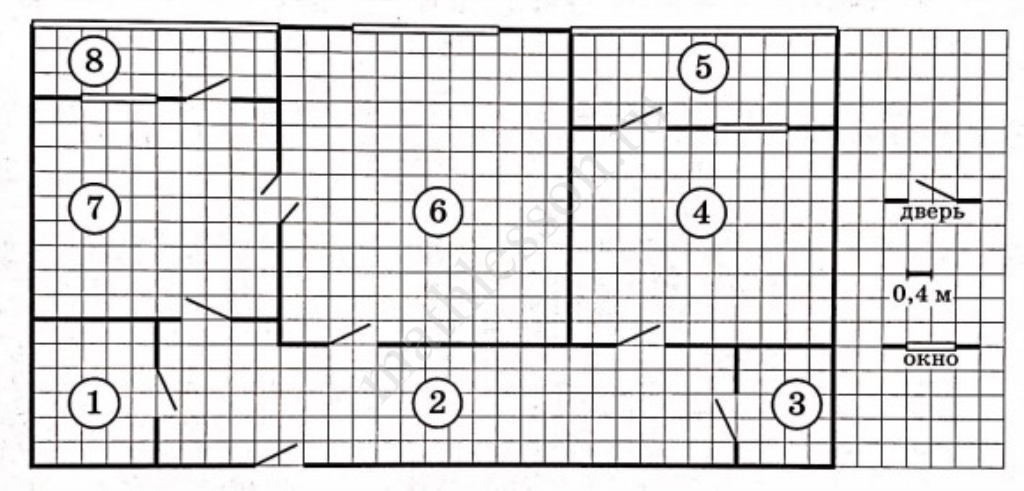
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Слева от входа в квартиру располагаются кухня и санузел, а также одна из застеклённых лоджий, в которую можно пройти из кухни. Также из кухни можно попасть в гостиную - самое большое по площади помещение. Наименьшую площадь в квартире имеет кладовая. В квартире есть ещё одна застеклённая лоджия, куда можно попасть, пройдя через спальню.
1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
| Помещения | кухня | спальня | санузел | кладовая | прихожая |
| Цифры |
2. Найдите ширину остекления лоджии, которая примыкает к спальне. Ответ дайте в сантиметрах.
3. Плитка для пола размером 20 см х 20 см продаётся в упаковках по 6 штук. Сколько упаковок плитки необходимо купить, чтобы выложить пол в обеих лоджиях?
4. Найдите площадь гостиной. Ответ дайте в квадратных метрах.
5. На сколько процентов площадь лоджии, примыкающей к спальне, больше площади кладовой?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$\left(\frac{3}{8}-\frac{1}{20}\right)\cdot 10$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Между какими целыми числами заключено число $$-\frac{130}{6}$$?
1) $$-19$$ и $$-20$$
2) $$-20$$ и $$-21$$
3) $$-21$$ и $$-22$$
4) $$-22$$ и $$-23$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\frac{3}{2} \cdot \sqrt{20} \cdot \sqrt{5}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$5x^2 + 15x = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Фабрика выпускает сумки. В среднем из $$120$$ сумок $$6$$ сумок имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется без дефекта.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Теорему косинусов можно записать в виде $$\cos \alpha = \frac{a^2 + b^2 - c^2}{2ab}$$, где $$a$$, $$b$$ и $$c$$ — стороны треугольника, а $$\alpha$$ — угол между сторонами $$a$$ и $$b$$. Пользуясь этой формулой, найдите величину $$\cos \alpha$$, если $$a = 5$$, $$b = 8$$ и $$c = 7$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$5x - x^2 \ge 0$$
1) $$[ 0;\ +\infty )$$
2) $$[ 0;\ 5 ]$$
3) $$[ 5;\ +\infty )$$
4) $$( -\infty;\ 0 ] \cup [ 5;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Врач прописал больному капли по следующей схеме: в первый день $$5$$ капель, а в каждый следующий день — на $$5$$ капель больше, чем в предыдущий, до тех пор, пока дневная доза не достигнет $$20$$ капель. Такую дневную дозу ($$20$$ капель) больной ежедневно принимает неделю, а затем уменьшает приём на $$5$$ капель в день до последнего дня, когда больной принимает последние $$10$$ капель. Сколько пузырьков лекарства нужно купить на весь курс, если в каждом пузырьке $$5$$ мл лекарства, то есть $$150$$ капель?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Периметр квадрата равен $$84$$. Найдите площадь этого квадрата.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
- Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
- Если диагонали параллелограмма равны, то он является ромбом.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$\frac{1}{(x - 3)^2} - \frac{3}{x - 3} - 4 = 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Сделаем замену: $$t = \frac{1}{x - 3}.$$ Получим квадратное уравнение: $$t^2 - 3t - 4 = 0.$$
2) Дискриминант: $$D = (-3)^2 - 4\cdot 1\cdot(-4) = 9 + 16 = 25,$$ $$t_{1,2} = \dfrac{3 \pm 5}{2}.$$ То есть: $$t_1 = 4,\qquad t_2 = -1.$$
3) Возвращаемся к $$x$$:
1) $$\frac{1}{x - 3} = 4,$$ $$x - 3 = \frac{1}{4},$$ $$x = \frac{13}{4} = 3{,}25.$$
2) $$\frac{1}{x - 3} = -1,$$ $$x - 3 = -1,$$ $$x = 2.$$
Задание 21
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось $$1$$ км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг $$3$$ минут назад. Найдите скорость (в км/ч) первого бегуна, если известно, что она на $$2$$ км/ч меньше скорости второго.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = 5|x - 2| - x^2 + 5x - 6$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Отрезки $$AB$$ и $$DC$$ лежат на параллельных прямых, а отрезки $$AC$$ и $$BD$$ пересекаются в точке $$M$$. Найдите $$MC$$, если $$AB=16$$, $$DC=24$$, $$AC=25$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Через точку $$O$$ пересечения диагоналей параллелограмма $$ABCD$$ проведена прямая, пересекающая стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Докажите, что отрезки $$AE=CF$$.
Треугольники AOE и COF равны по стороне и двум прилежащим к ней углам: AO = CO, поскольку диагонали параллелограмма точкой пересечения делятся пополам, $$\angle AOE=\angle COF$$ как вертикальные, $$\angle OAE=\angle OCF$$ как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей AC. Из равенства треугольников следует равенство их сходственных сторон: AE = CF. Что и требовалось доказать.
Задание 25
Биссектрисы углов $$A$$ и $$B$$ параллелограмма $$ABCD$$ пересекаются в точке $$K$$. Найдите площадь параллелограмма, если $$BC=7$$, а расстояние от точки $$K$$ до стороны $$AB$$ равно $$4$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!