ОГЭ 2023. Вариант 10 Ященко 36 вариантов ФИПИ школе.
Решаем 10 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 10 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Листы
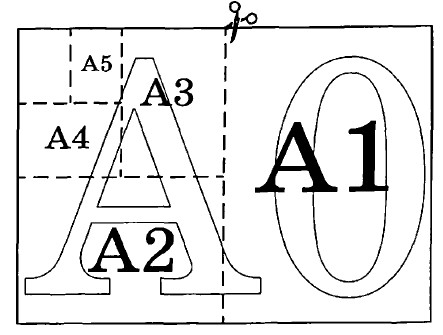
Общепринятые форматы листов бумаги обозначают буквой $$A$$ и цифрой: $$A0$$, $$A1$$, $$A2$$ и так далее. Площадь листа формата $$A0$$ равна 1 кв. м. Если лист формата $$A0$$разрезать пополам параллельно меньшей стороне, получаются два листа формата $$A1$$. Если так же лист $$A1$$ разрезать пополам, получаются два листа формата $$A2$$ и так далее.
Отношение длины листа к его ширине у всех форматов, обозначенных буквой $$A$$, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится). На практике размеры листа округляются до целого числа миллиметров.
В таблице 1 даны размеры листов бумаги четырёх форматов: от $$A3$$ до $$A6$$.
| порядковые номера | ширина (мм) | длина (мм) |
| 1 | 148 | 210 |
| 2 | 210 | 297 |
| 3 | 105 | 148 |
| 4 | 297 | 420 |
1. Для листов бумаги форматов $$A3$$, $$A4$$, $$A5$$ и $$A6$$ определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| формат бумаги | А3 | А4 | А5 | А6 |
| порядковые номера |
2. Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата $$A2$$?
3. Найдите длину большей стороны листа бумаги формата $$A2$$. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата $$A4$$. Ответ дайте в квадратных сантиметрах.
5. Бумагу формата $$A6$$ упаковали в пачки по $$320$$ листов. Найдите массу пачки, если масса бумаги площадью 1 кв. м равна $$108$$ г. Ответ дайте в граммах.
Задание 10
В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдёт приз в своей банке.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Основания трапеции равны $$7$$ и $$13$$. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$EM=\frac{1}{2}BC=3,5$$
$$MF=\frac{1}{2}AD=6,5$$
Задание 19
Какие из следующих утверждений верны?
- Сумма углов равнобедренного треугольника равна $$180^{\circ}$$ градусам.
- Боковые стороны любой трапеции равны.
- Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 20
Решите уравнение $$ (x^2 + x - 6)^2 + (x^2 - 9)^2 = 0 $$
1) Каждое слагаемое — квадрат, значит оно неотрицательно. Сумма двух квадратов равна нулю только тогда, когда оба квадрата равны нулю: $$ \begin{cases} x^2 - 16 = 0,\\ x^2 + 3x - 4 = 0. \end{cases} $$
2) Решим уравнение $$x^2 - 16 = 0.$$ Дискриминант: $$D = 0^2 - 4\cdot 1\cdot(-16) = 64,$$ $$x_{1,2} = \dfrac{0 \pm \sqrt{64}}{2} = \pm 4.$$ То есть $$x = 4,\ x = -4.$$
3) Решим уравнение $$x^2 + 3x - 4 = 0.$$ Дискриминант: $$D = 3^2 - 4\cdot 1\cdot(-4) = 9 + 16 = 25,$$ $$x_{1,2} = \dfrac{-3 \pm \sqrt{25}}{2} = \dfrac{-3 \pm 5}{2}.$$ Тогда $$x_1 = 1,\quad x_2 = -4.$$
4) Значение $$x$$ должно удовлетворять обоим уравнениям, общим корнем является только $$x = -4.$$