Задание 1698
Задание 1698
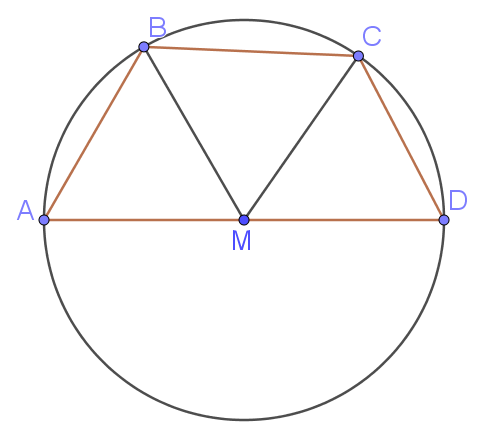
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$AD$$, если $$BC=19$$, а углы $$B$$ и $$C$$ четырёхугольника равны соответственно $$95^{\circ}$$ и $$115^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
Задание 2785
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$AD$$, если $$BC=12$$, а углы $$B$$ и $$C$$ четырёхугольника равны соответственно $$115^{\circ}$$ и $$95^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1711
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$AD$$, если $$BC=3$$, а углы $$B$$ и $$C$$ четырёхугольника равны соответственно $$94^{\circ}$$ и $$131^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2219
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$AD$$, если $$BC=10\sqrt{2}$$, а углы $$B$$ и $$C$$ четырёхугольника равны соответственно $$112^{\circ}$$ и $$113^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 101
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$BC$$, если $$AD = 12$$, а углы $$C$$ и $$D$$ четырёхугольника равны соответственно $$102^\circ$$ и $$72^\circ$$.
1) $$MA = MB = MC = MD$$, следовательно, около $$ABCD$$ можно описать окружность с центром $$M$$. Точка $$M$$ — середина $$AD$$, значит, $$AD$$ — диаметр этой окружности. Тогда $$AD = 12$$, откуда $$MA = MB = MC = MD = 6$$.
2) У вписанного четырёхугольника сумма противоположных углов равна $$180^\circ$$. Поэтому: $$\angle A = 180^\circ - \angle C = 180^\circ - 102^\circ = 78^\circ,$$ $$\angle B = 180^\circ - \angle D = 180^\circ - 72^\circ = 108^\circ.$$
3) Треугольник $$AMB$$ равнобедренный, так как $$MA = MB$$. Тогда $$\angle MAB = \angle ABM.$$ Но точка $$M$$ лежит на прямой $$AD$$, поэтому $$\angle MAB = \angle A = 78^\circ$$, значит, $$\angle ABM = 78^\circ.$$ Следовательно, $$\angle MBC = \angle B - \angle ABM = 108^\circ - 78^\circ = 30^\circ.$$
4) Треугольник $$BMC$$ тоже равнобедренный, так как $$MB = MC$$, значит $$\angle MBC = \angle BCM = 30^\circ.$$ Тогда $$\angle BMC = 180^\circ - 2\cdot 30^\circ = 120^\circ.$$
5) По теореме косинусов в треугольнике $$BMC$$: $$BC^2 = BM^2 + MC^2 - 2\cdot BM \cdot MC \cdot \cos \angle BMC.$$ Подставляем $$BM = MC = 6$$ и $$\cos 120^\circ = -\dfrac{1}{2}$$: $$BC^2 = 6^2 + 6^2 - 2\cdot 6\cdot 6 \cdot \left(-\frac{1}{2}\right) = 36 + 36 + 36 = 108,$$ $$BC = \sqrt{108} = 6\sqrt{3}$$
Ответ: $$BC = 6\sqrt{3}$$.
Задание 122
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$BC$$, если $$AD = 10$$, а углы $$C$$ и $$D$$ четырёхугольника равны соответственно $$110^\circ$$ и $$65^\circ$$.
1) $$MA = MB = MC = MD$$, следовательно, около $$ABCD$$ можно описать окружность с центром $$M$$. $$AD$$ - диаметр, $$AD = 10$$, $$MA = MB = MC = MD = 5$$
2) Угол $$C = 110^\circ$$, угол $$D = 65^\circ$$, тогда угол $$A = 180^\circ - 110^\circ = 70^\circ$$, угол $$B = 180^\circ - 65^\circ = 115^\circ$$
3) Треугольник $$AMB$$ - равнобедренный, тогда $$\angle ABM = \angle A = 70^\circ$$. Следовательно, $$\angle MBC = 115^\circ - 70^\circ = 45^\circ$$.
4) Треугольник $$BMC$$ - равнобедренный, тогда $$\angle MBC = \angle BCM = 45^\circ$$. Следовательно, $$\angle BMC = 180^\circ - 2\cdot 45^\circ = 90^\circ$$
5) По теореме косинусов: $$BC^2 = BM^2 + MC^2 - 2\cdot BM \cdot MC \cdot \cos BMC$$; $$BC = \sqrt{25 +25 - 2\cdot 25 \cdot 0} = \sqrt{50} = 5\sqrt{2}$$