ОГЭ 2022. Вариант 13 Ященко 36 вариантов ФИПИ школе.
Решаем 13 вариант ОГЭ Ященко 2022 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 13 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Шины
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
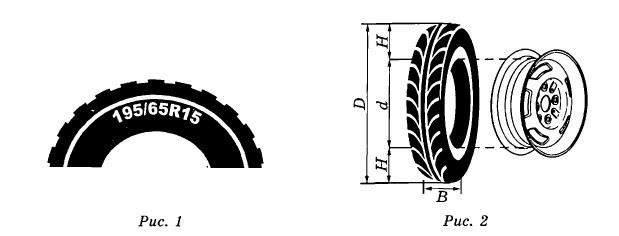
Для маркировки автомобильных шин применяется единая система обозначений. Например, $$195/65 R15$$ (рис. 1). Первое число (число $$195$$ в приведённом примере) обозначает дирину шины в миллиметрах (параметр $$B$$ на рисунке 2). Второе число (число $$65$$ в приведённом примере) - процентное отношение высоты боковины (параметр $$H$$ на рисунке 2) к ширине шины, то есть $$100 \cdot \frac{H}{B}$$.
Последующая буква обозначает тип конструкции шины. В данном примере буква $$R$$ означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса $$d$$ в дюймах (в одном дюйме $$25,4$$ мм). Таким образом, общий диаметр колеса $$D$$ легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки $$205/60 R16$$.
1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм)/Диаметр диска (дюймы) | 15 | 16 | 17 | 18 |
| 195 | 195/65 | 195/60 | 195/55 | не разр. |
| 205 | 205/60 | 205/55, 205/60 | 205/50 | 205/45 |
| 215 | 215/60 | 215/55 | 215/50 | 215/40, 215/45 |
| 225 | не разр. | 225/50 | 225/50, 225/45 | 225/40 |
Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен $$17$$ дюймам? Ответ дайте в миллиметрах.
2. На сколько миллиметров радиус колеса с маркировкой $$195/55 R17$$ больше, чем радиус колеса с маркировкой $$225/45 R17$$?
3. Найдите диаметр $$D$$ колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
4. На сколько миллиметров уменьшится диаметр $$D$$ колеса, если заменить шины, установленные на заводе, шинами с маркировкой $$225/40 R18$$?
5. На сколько процентов уменьшится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой $$225/40 R18$$? Округлите результат до десятых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Сколько целых чисел расположено между числами $$\sqrt{13}$$ и $$\sqrt{130}$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$(x - 1)(-x - 4) = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Общий вид линейной функции $$y=kx+b$$. При этом если $$k>0$$, то концы прямой находятся в первой и третьей координатных четвертях, если $$k<0$$, то во второй и четвертой. Если $$b>0$$, то прямая пересекает ось Оу над осью Ох, если $$b<0$$, то под осью. Получим:
- $$y=-\frac{2}{3}+4$$ - 2
- $$y=\frac{2}{3}x-4$$ - 1
- $$y=\frac{2}{3}x+4$$ - 3
Задание 11
При подготовке к экзамену Олег выучил $$40$$ билетов, а $$10$$ билетов не выучил. Найдите вероятность того, что ему попадётся выученный билет.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Закон Кулона можно записать в виде $$F = k \frac{q_1 q_2}{r^2}$$, где $$F$$ — сила взаимодействия зарядов (в ньютонах), $$q_1$$ и $$q_2$$ — величины зарядов (в кулонах), $$k$$ — коэффициент пропорциональности (в Н·м²/Кл²), а $$r$$ — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда $$q_1$$ (в кулонах), если $$k = 9 \cdot 10^9$$ Н·м²/Кл², $$q_2 = 0,002$$ Кл, $$r = 2000$$ м, $$F = 0,00135$$ Н.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Найдите решение системы неравенств:
$$\left\{\begin{aligned}x + 0,6 &\le 0\\x - 1 &\ge -4\end{aligned}\right.$$
1) $$( -\infty;\ -3 ]$$
2) $$[ -0,6;\ +\infty )$$
3) $$( -\infty;\ -3 ];\ [ -0,6;\ +\infty )$$
4) $$[ -3;\ -0,6 ]$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
При проведении химического опыта реагент равномерно охлаждали на $$7,5^\circ\text{С}$$ в минуту. Найдите температуру реагента (в градусах Цельсия) спустя $$6$$ минут после начала проведения опыта, если начальная температура составляла $$-8,7^\circ\text{С}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
- Средняя линия трапеции равна сумме её оснований.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- верно, по признаку подобия треугольников;
- неверно, они могут и не пересекаться;
- неверно, средняя линия трапеции равна полусумме её оснований;
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Заметим, что $$x^2 + 6x + 9 = (x + 3)^2.$$ Тогда: $$(x - 1)(x + 3)^2 = 5(x + 3).$$ Вынесем общий множитель: $$(x + 3)\bigl((x - 1)(x + 3) - 5\bigr) = 0.$$ Отсюда либо $$x + 3 = 0,$$ либо $$(x - 1)(x + 3) - 5 = 0.$$
2) Первый корень: $$x = -3.$$
3) Решаем второе уравнение: $$(x - 1)(x + 3) - 5 = 0,$$ $$x^2 + 2x - 3 - 5 = 0,$$ $$x^2 + 2x - 8 = 0.$$ Дискриминант: $$D = 2^2 - 4\cdot 1\cdot(-8) = 4 + 32 = 36.$$ Корни: $$x_{1,2} = \frac{-2 \pm \sqrt{36}}{2} = \frac{-2 \pm 6}{2},$$ $$x_1 = 2,\qquad x_2 = -4.$$
Задание 21
Имеются два сосуда, содержащие $$12$$ кг и $$8$$ кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий $$65 \%$$ кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать $$60 \%$$ кислоты. Сколько процентов кислоты содержится во втором растворе?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \frac{2|x| - 1}{|x| - 2x^2}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


ОДЗ: $$\left | x \right |-2x^{2}\neq 0\Leftrightarrow$$ $$\left | x \right |-2\left | x \right |^{2} \neq 0\Leftrightarrow$$ $$\left | x \right |(1-2\left | x \right |)\neq 0\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 0\\ x\neq 0,5\\ x\neq -0,5\end{matrix}\right.$$.
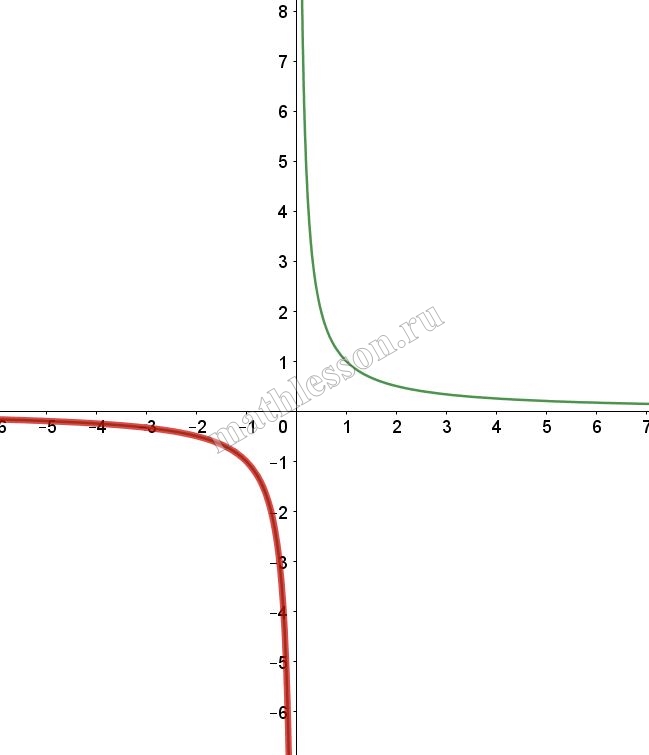
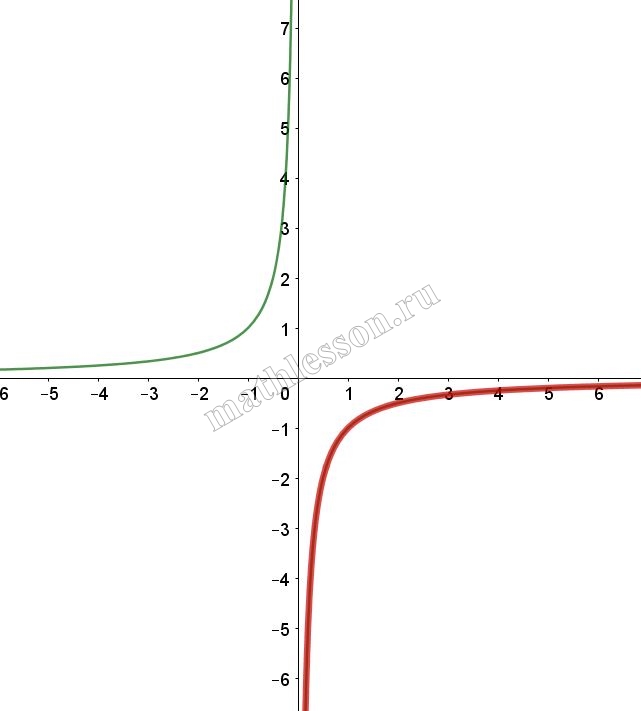
При $$x>0$$: $$y=\frac{2x-1}{x(1-2x)}=-\frac{1}{x}$$ (выдерена красным)
При $$x<0$$: $$y=\frac{-2x-1}{-x-2x^{2}}=\frac{1}{x}$$(выделена красным)
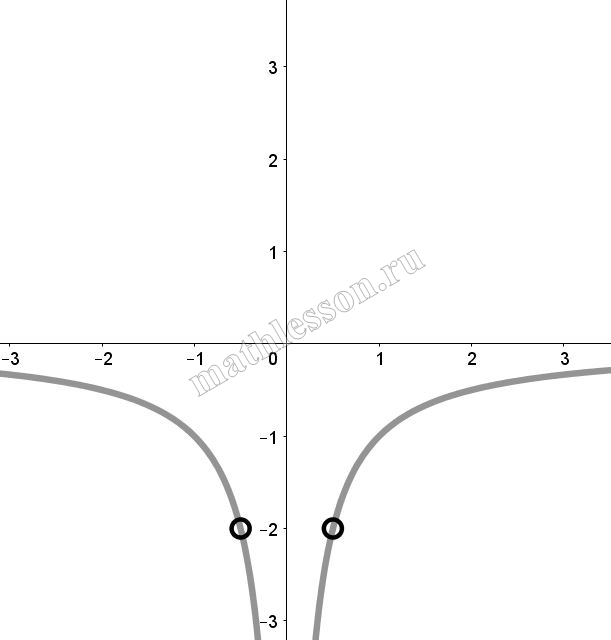
Итоговый график с учетом ОДЗ:
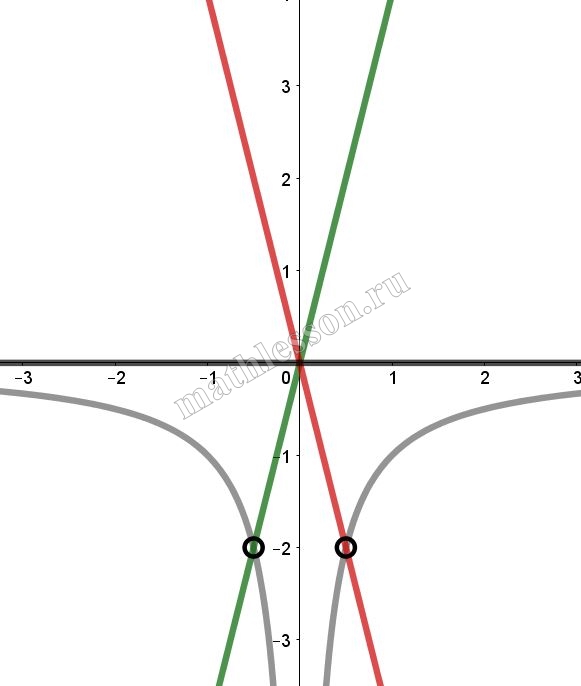
Найдем k: $$y=kx$$ проходит через (-0,5 ; -2): $$-2=-0,5*k\Rightarrow k=4$$(зеленая) и через (0,5; -2): $$-2=0,5k\Rightarrow k=-4$$(красная). При k=0 (черная) тоже не имеет пересечений
Задание 23
Высота $$AH$$ ромба $$ABCD$$ делит сторону $$CD$$ на отрезки $$DH=20$$ и $$CH=5$$. Найдите высоту ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!