ОГЭ 2026. Вариант 6 Ященко 36 вариантов ФИПИ школе.
Решаем 6 вариант ОГЭ Ященко 2026 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 6 варианта (всех заданий) Ященко 2026 ФИПИ 36 вариантов.
Рутуб
Ютуб
Задания:
Задание 1-5
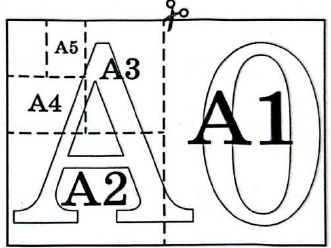
Общепринятые форматы листов бумаги обозначают буквой $$A$$ и цифрой: $$A0$$, $$A1$$, $$A2$$ и так далее. Лист формата $$A0$$ имеет форму прямоугольника, площадь которого равна $$1\ \text{кв. м}$$. Если лист формата $$A0$$ разрезать пополам параллельно меньшей стороне, получатся два одинаковых листа формата $$A1$$. Если лист $$A1$$ разрезать пополам таким же образом, получатся два листа формата $$A2$$. И так далее.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это нужно, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
1.В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы $$A1$$, $$A2$$, $$A4$$ и $$A6$$.
| Номер листа | Длина (мм) | Ширина (мм) |
|---|---|---|
| 1 | 148 | 105 |
| 2 | 594 | 420 |
| 3 | 297 | 210 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. Заполните таблицу. В бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
| Форматы бумаги | A6 | A4 | A2 | A1 |
|---|---|---|---|---|
| Порядковые номера |
2. Сколько листов формата $$A7$$ получится из одного листа формата $$A4$$?
3. Найдите площадь листа формата $$A5$$. Ответ дайте в квадратных сантиметрах и округлите до ближайшего целого числа, кратного $$10$$.
4. Найдите ширину листа бумаги формата $$A7$$. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного $$5$$.
5. Бумагу формата $$A6$$ упаковали в пачки по $$350$$ листов. Найдите массу пачки, если масса бумаги площадью $$1\ \text{кв. м}$$ равна $$96$$ г. Ответ дайте в граммах.
1) Приведём знаменатель: $$\frac{1}{3} - 1 = \frac{1}{3} - \frac{3}{3} = -\frac{2}{3}.$$
2) Деление заменим умножением: $$2,8 \cdot \left(-\frac{3}{2}\right).$$
3) Запишем \(2,8 = \frac{28}{10}\). Тогда: $$\frac{28}{10} \cdot \left(-\frac{3}{2}\right) = -\frac{84}{20} = -4,2.$$
Задание 8
Найдите значение выражения $$(\sqrt{112} + \sqrt{7}) \cdot \sqrt{7}$$.
1) Раскроем скобки: $$(\sqrt{112} + \sqrt{7})\cdot\sqrt{7} = \sqrt{112}\cdot\sqrt{7} + \sqrt{7}\cdot\sqrt{7}.$$
2) Используем свойство $$\sqrt{a}\cdot\sqrt{b} = \sqrt{ab}$$: $$\sqrt{112}\cdot\sqrt{7} = \sqrt{112\cdot 7} = \sqrt{784},$$ а также $$\sqrt{7}\cdot\sqrt{7} = 7.$$ Тогда $$(\sqrt{112} + \sqrt{7})\cdot\sqrt{7} = \sqrt{784} + 7.$$
3) Так как $$\sqrt{784} = 28,$$ получаем: $$28 + 7 = 35.$$
Задание 9
Решите уравнение $$25 - x^2 = 0$$. Если уравнение имеет больше одного корня, в ответ запишите меньший из корней.
1) Перенесём $$x^2$$. Тогда: $$25 = x^2.$$
2) Находим корни: $$x^2 = 25 \Rightarrow$$ $$x = \pm \sqrt{25} \Rightarrow$$ $$x = \pm 5$$. Меньшее значение: $$x = -5.$$
Задание 10
В девятом классе учатся $$14$$ мальчиков и $$11$$ девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
1) Общее количество учеников: $$14 + 11 = 25.$$
2) Вероятность выбрать мальчика: $$P = \frac{14}{25} = 0{,}56.$$
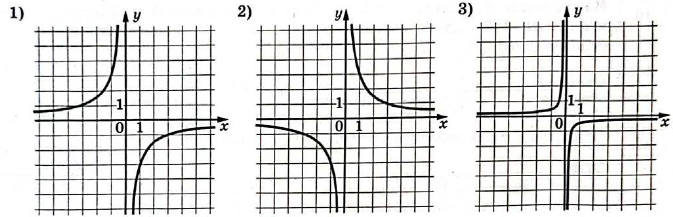
1) По знаку коэффициента определяем четверти:
- Функция $$y = \frac{3}{x}$$ (буква $$A$$) имеет ветви в первой и третьей четвертях. То есть это график под номером $$2$$.
- Функции $$y = -\frac{3}{x}$$ и $$y = -\frac{1}{3x}$$ (буквы $$\text{Б}$$ и $$B$$) имеют ветви во второй и четвёртой четвертях.
2) Сравним модуль коэффициента.
- У $$y = -\frac{3}{x}$$ модуль коэффициента больше, чем у $$y = -\frac{1}{3x}$$, поэтому график с ветвями во второй и четвёртой четвертях, расположенными дальше от осей, соответствует букве $$\text{Б}$$. То есть $$\text{Б}$$ это $$1$$ график.
- Оставшийся график под номером $$3$$ во второй и четвёртой четвертях — для буквы $$B$$.
Задание 12
Кинетическая энергия тела $$E$$ (в джоулях) вычисляется по формуле $$E = \frac{m v^2}{2}$$, где $$m$$ — масса тела (в килограммах), а $$v$$ — его скорость (в м/с). Пользуясь этой формулой, найдите скорость автомобиля массой $$800$$ кг, если известно, что его кинетическая энергия равна $$810$$ тысяч джоулей. Ответ дайте в метрах в секунду.
1) Запишем данные: $$m = 800$$ кг, $$E = 810000$$ Дж.
2) Выразим скорость: $$v^2 = \frac{2E}{m}.$$
3) Подставим значения: $$v^2 = \frac{2\cdot 810000}{800} = \frac{1620000}{800} = 2025.$$
4) Найдём скорость: $$v = \sqrt{2025} = 45.$$
Задание 13
Укажите решение неравенства: $$9 - 5x 7x + 15$$
1) $$(-\infty;\,-0{,}5)$$
2) $$(3;\,+\infty)$$
3) $$(-0{,}5;\,+\infty)$$
4) $$(-\infty;\,3)$$
1) Перенесём слагаемые: $$9 - 15 7x + 5x,$$ $$-6 12x.$$
2) Делим обе части на $$12$$ (число положительное, знак не меняется): $$x > -\frac{6}{12} = -\frac{1}{2} = -0,5.$$
3) Запишем ответ: $$x \in (-0,5;\,+\infty).$$ То есть $$3$$ вариант ответа.
Задание 14
На высоте $$2205$$ м над уровнем моря атмосферное давление составляет $$550$$ мм рт. ст. Считая, что при подъёме на каждые $$10{,}5$$ м давление уменьшается примерно на $$1$$ мм рт. ст., определите атмосферное давление на высоте $$1785$$ м над уровнем моря.
1) Определим изменение высоты: $$1785 - 2205 = -420$$ м. Это означает, что мы опускаемся на $$420$$ м.
2) На каждые $$10,5$$ м давление изменяется на $$1$$ мм рт. ст., значит изменение давления: $$\frac{420}{10,5} = 40$$ мм рт. ст. При снижении высоты давление увеличивается: $$550 + 40 = 590$$ мм рт. ст.
Задание 15
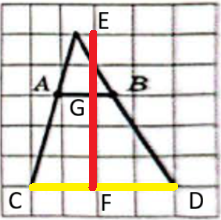
В треугольнике $$ABC$$ угол $$C$$ равен $$90^\circ$$, $$M$$ — середина стороны $$AB$$, $$AB = 50$$, $$AC = 30$$. Найдите $$CM$$.
1) Угол $$C$$ прямой, значит сторона $$AB$$ — гипотенуза.
2) В прямоугольном треугольнике середина гипотенузы равноудалена от всех вершин: $$CM = AM = BM.$$
3) Поскольку $$M$$ — середина $$AB$$, $$AM = BM = \frac{AB}{2} = \frac{50}{2} = 25,$$ следовательно, $$CM = 25.$$
Задание 16
На окружности с центром в точке $$O$$ отмечены точки $$A$$ и $$B$$ так, что $$\angle AOB = 132^\circ$$. Длина меньшей дуги $$AB$$ равна $$22$$. Найдите длину большей дуги $$AB$$.
1) Меньшей дуге соответствует угол $$132^\circ,$$ всей окружности — $$360^\circ,$$ значит длина всей окружности: $$L = 22 \cdot \frac{360^\circ}{132^\circ}.$$
2) Сократим дробь: $$\frac{360}{132} = \frac{30}{11},\quad L = 22 \cdot \frac{30}{11} = 60.$$
3) Большая дуга: $$L_{\text{большой дуги}} = 60 - 22 = 38.$$
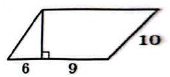
1) По рисунку основание параллелограмма равно $$a = 6 + 9 = 15,$$ а боковая сторона равна $$10.$$ Эта сторона вместе с отрезком основания длиной $$6$$ образует прямоугольный треугольник, поэтому высота параллелограмма — второй катет этого треугольника.
2) Найдём высоту из прямоугольного треугольника: $$h^2 + 6^2 = 10^2,$$ $$h^2 = 100 - 36 = 64,$$ $$h = 8.$$
3) Площадь параллелограмма: $$S = a \cdot h = 15 \cdot 8 = 120.$$
Задание 19
Какое из следующих утверждений является истинным высказыванием?
- Сумма углов прямоугольного треугольника равна $$90$$ градусам.
- Если в ромбе один из углов равен $$90$$ градусам, то этот ромб является квадратом.
- Две окружности всегда пересекаются, если радиус одной окружности больше радиуса другой окружности.
В ответе запишите номер выбранного утверждения.
Задание 20
Решите систему уравнений: $$ \left\{ \begin{aligned} x^2 + y^2 = 68, \\ xy = -16. \end{aligned} \right. $$
1) Из второго уравнения: $$y = \dfrac{-16}{x},\qquad x \ne 0.$$ Подставим в первое: $$x^2 + \left(\dfrac{-16}{x}\right)^2 = 68.$$ Умножим на $$x^2$$. Тогда: $$x^2\cdot x^2 + 256 = 68x^2,$$ $$x^4 + 256 = 68x^2.$$ Переносим: $$x^4 - 68x^2 + 256 = 0.$$ Пусть $$t = x^2$$, тогда $$t^2 - 68t + 256 = 0.$$
2) Дискриминант: $$D = 68^2 - 4\cdot 256 = 4624 - 1024 = 3600.$$ Корни: $$t_{1,2} = \dfrac{68 \pm \sqrt{3600}}{2} = \dfrac{68 \pm 60}{2}.$$ Получаем: $$t_1 = 64,\qquad t_2 = 4.$$ То есть $$x^2 = 64,\qquad x^2 = 4,$$ откуда $$x = \pm 8,\qquad x = \pm 2.$$
3) Находим $$y = \dfrac{-16}{x}.$$ Если $$x = 8,$$ то $$y = -2.$$ Если $$x = -8,$$ то $$y = 2.$$ Если $$x = 2,$$ то $$y = -8.$$ Если $$x = -2,$$ то $$y = 8.$$
Задание 21
Теплоход проходит по течению реки до пункта назначения $$240$$ км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна $$22$$ км/ч, стоянка длится $$10$$ часов, а в пункт отправления теплоход возвращается через $$32$$ часа после отплытия из него.
1) Пусть скорость течения равна $$u$$ км/ч.
Тогда по течению скорость: $$22 + u,$$ против течения: $$22 - u.$$ Время в пути: $$t_1 = \frac{240}{22 + u},\quad t_2 = \frac{240}{22 - u}.$$ По условию: $$t_1 + t_2 + 10 = 32,$$ то есть $$\frac{240}{22 + u} + \frac{240}{22 - u} = 22.$$
2) Приведём к общему знаменателю: $$\frac{240(22 - u) + 240(22 + u)}{22^2 - u^2} = 22,$$ $$\frac{240\cdot 44}{484 - u^2} = 22.$$
3) Решим: $$240\cdot 44 = 22(484 - u^2),$$ $$10560 = 10648 - 22u^2,$$ $$22u^2 = 10648 - 10560 = 88,$$ $$u^2 = 4,\quad u = 2.$$ Берём положительное значение.
Задание 22
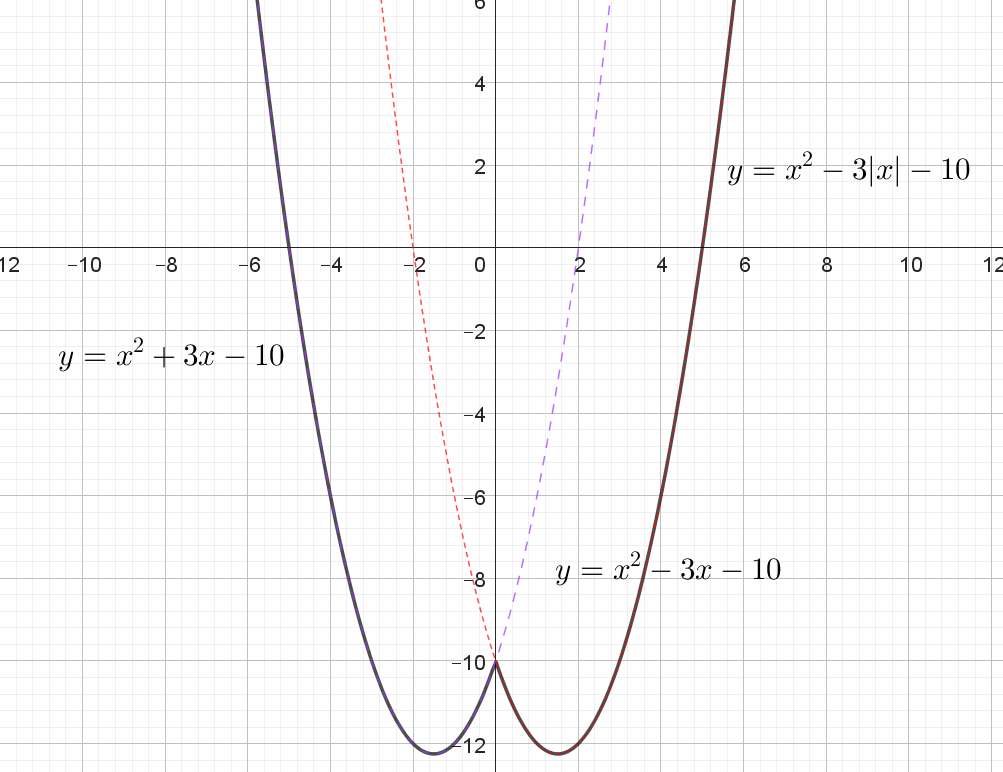
Постройте график функции $$y = x^2 - 3|x| - 10$$. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
1) Раскроем модуль:
При $$x \ge 0$$: $$y = x^2 - 3x - 10.$$ (красный пунктир) При $$x < 0$$: $$y = x^2 + 3x - 10$$ (синий пунктир).
Это две параболы, открытые вверх.
Первая имеет вершину при $$x = \frac{3}{2},$$ вторая — при $$x = -\frac{3}{2}.$$ Обе вершины принадлежат своим областям: первая — к $$x \ge 0,$$ вторая — к $$x < 0.$$ Поэтому на графике функции каждая парабола присутствует почти целиком (обрезана только по другую сторону от нуля).
2) Горизонтальная прямая $$y = k$$ может пересекать каждую параболу максимум в двух точках. Для значений $$k$$, лежащих выше обеих вершин (достаточно взять $$k$$ больше наибольшего из минимальных значений функций), прямая пересечёт каждую параболу в двух точках.
Следовательно, всего возможны четыре точки пересечения.
Задание 23
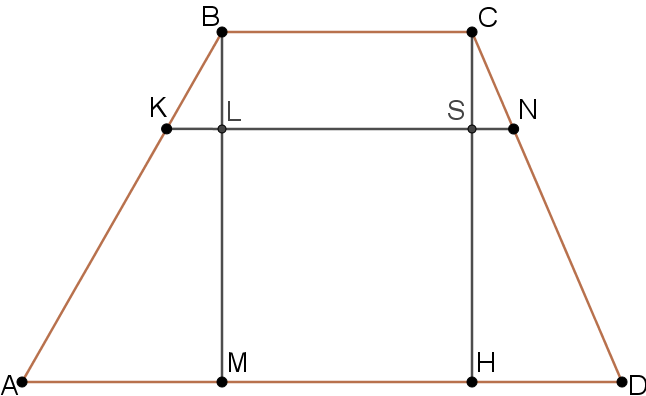
Прямая, параллельная основаниям трапеции $$ABCD$$, пересекает её боковые стороны $$AB$$ и $$CD$$ в точках $$K$$ и $$N$$ соответственно. Найдите длину отрезка $$KN$$, если $$AD = 40$$, $$BC = 16$$, $$CN = 12$$, $$ND = 18$$.
1) Проведём высоты: пусть $$CH \perp AD$$, $$BM \perp AD$$. Обозначим точки пересечения: $$CH \cap KN = S$$, $$BM \cap KN = L$$.
2) Так как $$KN \parallel AD$$, то углы $$\angle CNS = \angle CDH$$ (соответственные), а также $$\angle CSN = \angle CHD = 90^\circ$$. Следовательно, треугольники $$CNS$$ и $$CDH$$ подобны.
Длина стороны $$CD$$: $$CD = CN + ND = 12 + 18 = 30.$$ Из подобия: $$\frac{SN}{HD} = \frac{CN}{CD} = \frac{12}{30}.$$ Отсюда: $$SN = \frac{12}{30}\,HD.$$
3) Аналогично пункту 2: треугольники $$BKL$$ и $$BAM$$ подобны, поэтому $$KL = \frac{12}{30}\,AM.$$ Кроме того, выполняется равенство $$BC = LS = MH$$ (прямоугольники), а значит $$BC = LS = MH = 16.$$
4) Тогда $$AM + HD = AD - MH = 40 - 16 = 24.$$
5) Теперь длина отрезка $$KN$$: $$KN = KL + LS + SN = \frac{12}{30}(AM + HD) + 16 = \frac{12}{30}\cdot 24 + 16 = 9{,}6 + 16 = 25{,}6.$$
Ответ: $$25{,}6.$$
Задание 24
В остроугольном треугольнике $$ABC$$ проведены высоты $$AH$$ и $$CF$$. Докажите, что углы $$CFH$$ и $$CAH$$ равны.
1) Пусть $$AH \cap CF = M$$, тогда углы $$\angle FMA$$ и $$\angle HMC$$ вертикальные: $$\angle FMA = \angle HMC.$$
2) Так как $$AH$$ и $$CF$$ — высоты, то $$\angle AFM = 90^\circ,\quad \angle MHC = 90^\circ.$$ Следовательно, $$\triangle AFM \sim \triangle CHM,$$ откуда $$\frac{FM}{HM} = \frac{AM}{MC}$$($$\ast$$).
3) Углы $$\angle FMH$$ и $$\angle AMC$$ вертикальные, поэтому $$\angle FMH = \angle AMC.$$ С учётом ($$\ast$$) получаем подобие $$\triangle FMH \sim \triangle AMC,$$ откуда $$\angle CFH = \angle CAH,$$ так как лучи $$FC$$ и $$FM$$, а также $$AH$$ и $$AM$$ являются продолжениями друг друга.
Задание 25
Биссектрисы углов $$B$$ и $$C$$ параллелограмма $$ABCD$$ пересекаются в точке $$E$$. Найдите площадь параллелограмма, если $$AB = 14$$, а расстояние от точки $$E$$ до стороны $$BC$$ равно $$7{,}5$$.
1. Опустим перпендикуляры $$EF$$, $$EH$$ и $$EG$$ из точки $$E$$ соответственно на прямые $$BC$$, $$AB$$ и $$CD$$ как показано на рисунке.
2. По свойству биссектрисы: для $$\angle B$$ получим $$FE = EH = 7,5$$, а для $$\angle C$$ - $$GE = EH = 7,5$$
3. Так как $$AB \parallel CD$$, а $$EF$$ и $$EG$$ перпендикуляры к ним и имеют общую точку, то $$F$$, $$E$$, $$G$$ лежат на одной прямой, а отрезок $$FG$$ является высотой для параллелограмма.
4. $$S_{ABCD} = AB \cdot FG = 14 \cdot 15 = 210$$