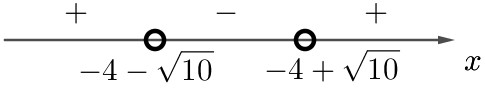ОГЭ 2023. Вариант 25 Ященко 36 вариантов ФИПИ школе.
Решаем 25 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 25 варианта (всех заданий) Ященко 2023 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Листы
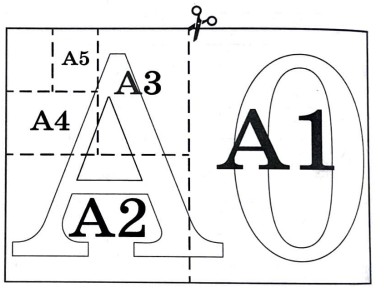
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: A0, A1, А2 и так далее. Площадь листа формата АО равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата A1. Если так же лист A1 разрезать пополам, получаются два листа формата А2 и так далее.
Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны. друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится). На практике размеры листа округляются до целого числа миллиметров. В таблице 1 даны размеры листов бумаги четырёх форматов: от А3 до А6.
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 210 | 297 |
| 2 | 297 | 420 |
| 3 | 105 | 148 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов А6, А5, А4 и А3 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А6 | А5 | А4 | Ф3 |
2. Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата A0?
3. Найдите длину меньшей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата А5. Ответ дайте в квадратных сантиметрах.
5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$\sqrt{0,36p^4q^8}$$, при $$p = 5$$ и $$q = 2$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 + 8x + 15 = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Закон Джоуля–Ленца можно записать в виде $$Q = I^2 R t$$, где $$Q$$ — количество теплоты (в джоулях), $$I$$ — сила тока (в амперах), $$R$$ — сопротивление цепи (в омах), а $$t$$ — время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи $$R$$ (в омах), если $$Q = 1296$$ Дж, $$I = 9$$ А, $$t = 2$$ с.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$(x + 2)(x - 10) > 0$$
1) $$( -2;\ 0 )$$
2) $$( -\infty;\ -2 ) \cup ( 10;\ +\infty )$$
3) $$( 10;\ +\infty )$$
4) $$( -2;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В амфитеатре $$20$$ рядов. В первом ряду $$56$$ мест, а в каждом следующем — на $$2$$ места меньше, чем в предыдущем. Сколько всего мест в амфитеатре?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Площадь параллелограмма можно найти по формуле $$S=a\cdot h$$, где $$a$$ - длина стороны параллелограмма, $$h$$ - длина высоты, проведенной к этой стороне.
$$S=(3+5)\cdot 12=96$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите неравенство: $$\frac{-18}{(x+4)^2 - 10} \ge 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Числитель $$-18$$ — отрицательное и не равен нулю, значит дробь никогда не обращается в ноль. Чтобы дробь была положительной, знаменатель должен быть отрицательным: $$(x+4)^2 - 10 < 0.$$
2) Решим неравенство: $$(x+4)^2 - 10 < 0.$$ Учтём, что $$(x+4)^2 - 10 = (x + 4)^2 - (\sqrt{10})^2 = (x+4-\sqrt{10})(x+4+\sqrt{10}).$$ Нули $$x_1 = -4 - \sqrt{10};\quad x_2 = -4 + \sqrt{10}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x+4-\sqrt{10})(x+4+\sqrt{10})$$ на полученных промежутках:
Выражение отрицательное при: $$x \in (-4-\sqrt{10};\,-4+\sqrt{10}).$$
Задание 21
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на $$51$$ минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет $$251$$ км, скорость первого велосипедиста равна $$10$$ км/ч, скорость второго — $$20$$ км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \frac{(x + 3)(x^2 - 3x + 2)}{x - 2}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
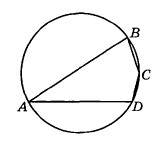
Окружность пересекает стороны $$AB$$ и $$AC$$ треугольника $$ABC$$ в точках $$K$$ и $$P$$ соответственно и проходит через вершины $$B$$ и $$C$$. Найдите длину отрезка $$KP$$, если $$AP=34$$, а сторона $$BC$$ в $$2$$ раза меньше стороны $$AB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
Углы при одном из оснований трапеции равны $$53^{\circ}$$ и $$37^{\circ}$$, а отрезки, соединяющие середины противоположных сторон трапеции, равны $$6$$ и $$2$$. Найдите основания трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!