Задание 4240
Задание 4240
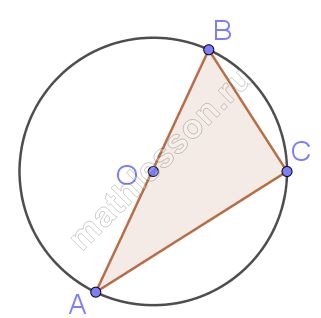
В треугольнике $$ABC$$ $$AC = 3\sqrt{7}$$, $$BC = 3\sqrt{2}$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус окружности, описанной около этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Радиус описанной вокруг прямоугольного треугольника окружности равен половине длины его гипотенузы. Найдем гипотенузу по теореме Пифагора: $$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{9*7+9*2}=9$$ В таком случае радиус будет равен 9/2 = 4,5
Аналоги к этому заданию:
Задание 4889
В треугольнике $$ABC$$ угол $$C$$ равен $$90^\circ$$, $$AC = 30$$, $$BC = 5\sqrt{13}$$. Найдите радиус окружности, описанной около этого треугольника.
1) По теореме Пифагора $$AB=\sqrt{30^{2}+(5\sqrt{13})^{2}}=35$$
2) По свойству прямоугольного треугольника, радиус описанной окружности равен половине гипотенузы, то есть $$R=\frac{35}{2}=17,5$$
Задание 2813
В треугольнике $$ABC$$ известно, что $$AC = 24$$, $$BC = \sqrt{365}$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус описанной окружности этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 110
В треугольнике $$ABC$$ известно, что $$AC = 20$$, $$BC = 15$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус описанной около этого треугольника окружности.
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы
Гипотенуза $$AB = \sqrt{AC^2 + BC^2} = \sqrt{400 + 225} = \sqrt{625} = 25$$
$$R = \frac{25}{2} = 12,5$$
Задание 131
В треугольнике $$ABC$$ известно, что $$AC = 12$$, $$BC = 35$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус описанной около этого треугольника окружности.
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы
Гипотенуза $$AB = \sqrt{AC^2 + BC^2} = \sqrt{144 + 1225} = \sqrt{1369} = 37$$
$$R = \frac{37}{2} = 18,5$$