ОГЭ 2021. Вариант 12 Ященко 36 вариантов ФИПИ школе.
Решаем 12 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 12 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Найдите значение выражения $$b^{12} \cdot (b^{-3})^3$$ при $$b = 5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Решите уравнение: $$5x^2 + 4x - 1 = 0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с зелёным чаем в $$7$$ раз меньше, чем с чёрным. Найдите вероятность того, что случайно выбранный пакетик окажется с чёрным чаем.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


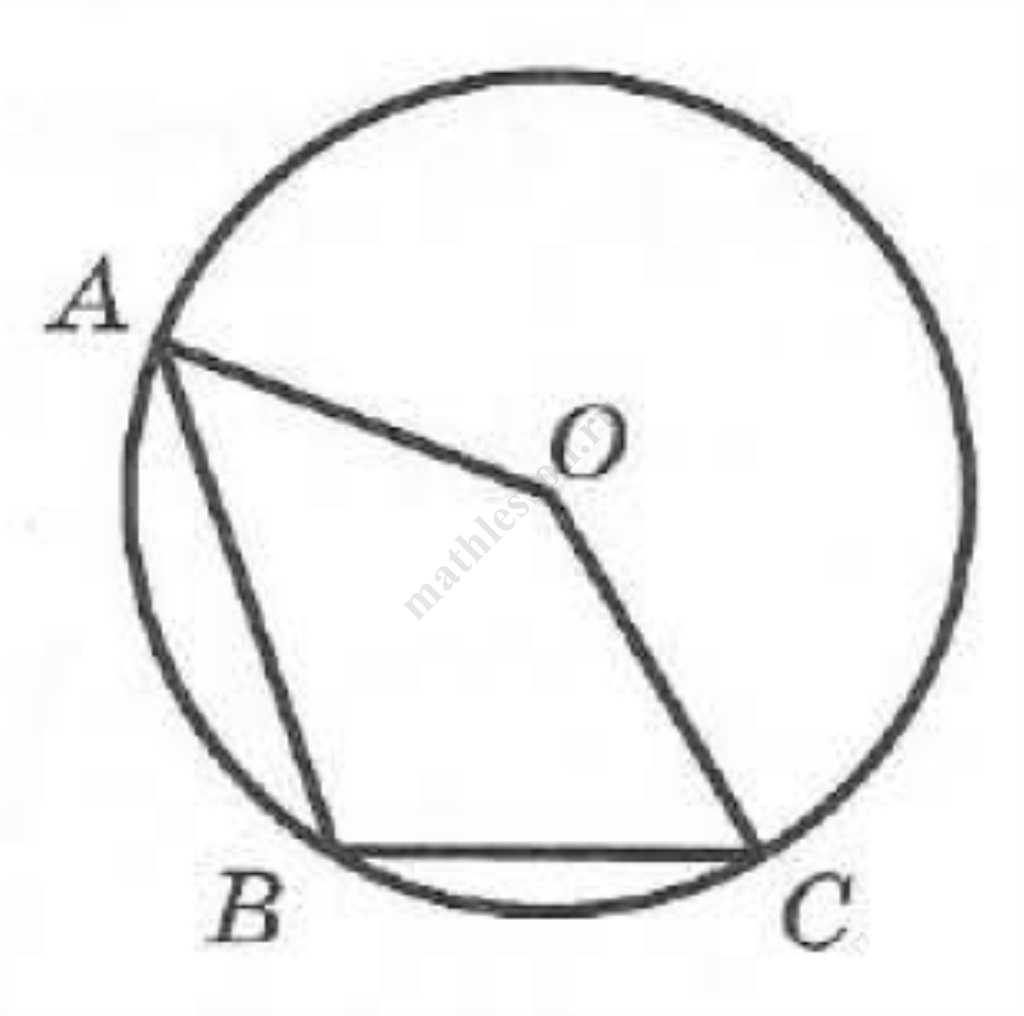
Задание 11
Радиус окружности, описанной около треугольника, можно вычислить по формуле $$R = \frac{a}{2 \sin \alpha}$$, где $$a$$ — сторона, а $$\alpha$$ — противолежащий ей угол треугольника. Пользуясь этой формулой, найдите $$a$$, если $$R = 10$$ и $$\sin \alpha = \frac{3}{20}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Укажите решение неравенства: $$5x + 4 x + 6$$
1) $$( -\infty;\ 0,5 )$$
2) $$( 2,5;\ +\infty )$$
3) $$( -\infty;\ 2,5 )$$
4) $$( 0,5;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Каждое простейшее одноклеточное животное — инфузория-туфелька — размножается делением на $$2$$ части. Сколько инфузорий было первоначально, если после пятикратного деления их стало $$960$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Катеты прямоугольного треугольника равны $$16$$ и $$30$$. Найдите гипотенузу этого треугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


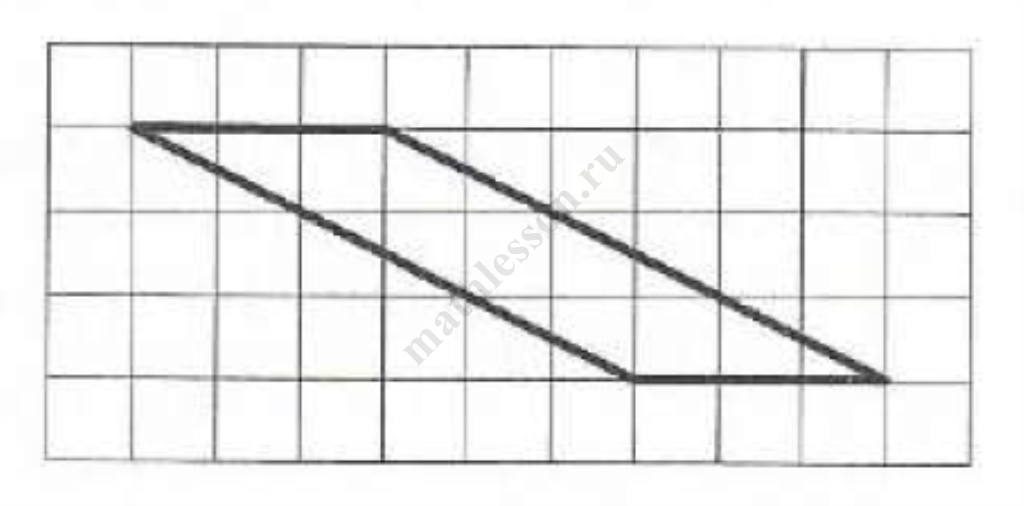
Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Какие из следующих утверждений верны?
- Если диагонали параллелограмма равны, то он является ромбом.
- Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
- В любом тупоугольном треугольнике есть острый угол.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Группируем: $$x^3 + 4x^2 - x - 4 = x^2(x+4) - 1(x+4).$$
2) Выносим общий множитель: $$(x+4)(x^2 - 1) = 0.$$
3) Раскладываем квадратный множитель: $$x^2 - 1 = (x-1)(x+1),$$ получаем $$(x+4)(x-1)(x+1) = 0.$$
4) Приравниваем множители к нулю: $$x+4 = 0,\quad x-1 = 0,\quad x+1 = 0,$$ откуда $$x = -4,\; 1,\; -1.$$
Задание 20
Грузовик перевозит партию щебня массой $$340$$ тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено $$4$$ тонны щебня. Определите, сколько тонн щебня было перевезено за последний день, если вся работа была выполнена за $$17$$ дней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


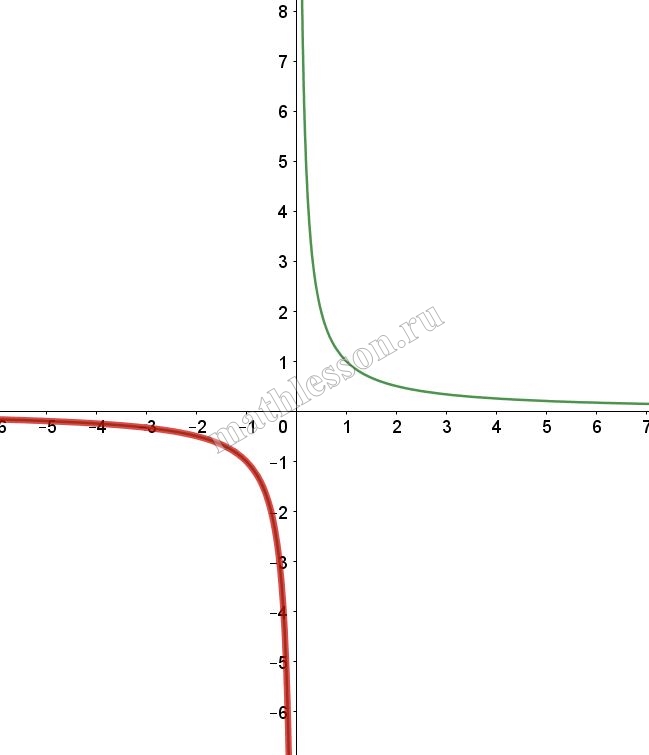
Задание 21
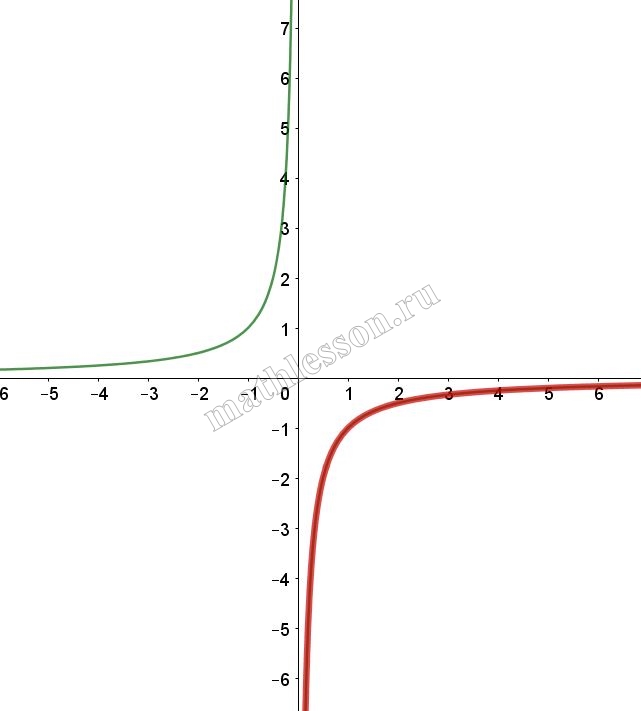
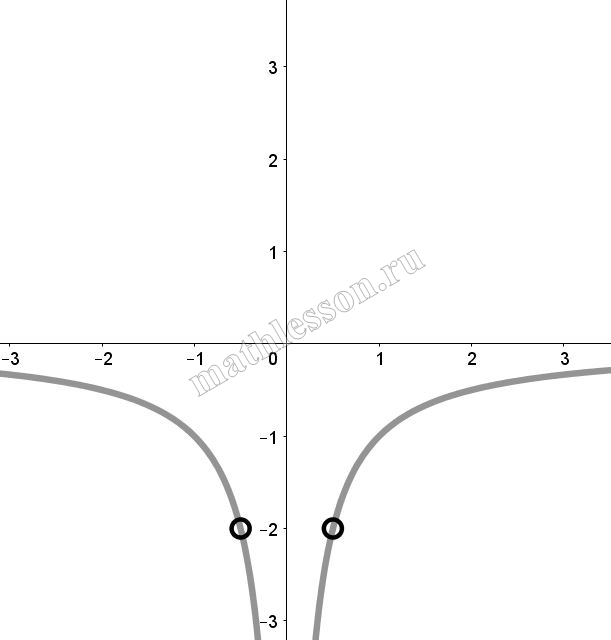
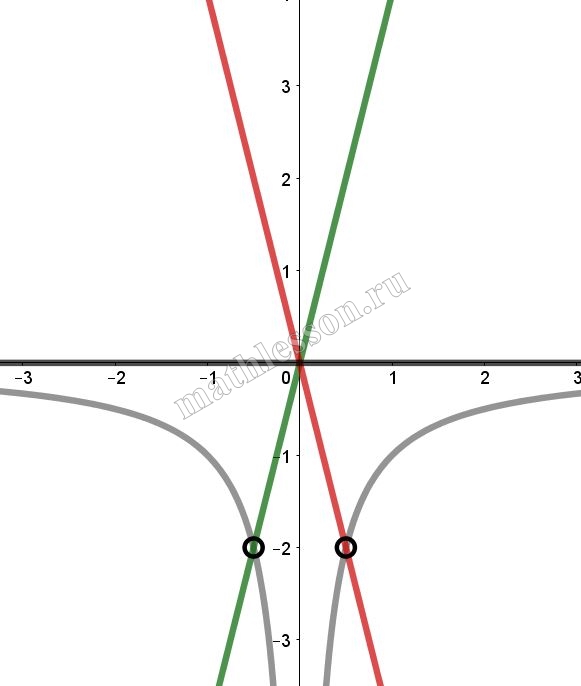
Постройте график функции $$y = \frac{2|x| - 1}{|x| - 2x^2}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ не имеет с графиком ни одной общей точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


ОДЗ: $$\left | x \right |-2x^{2}\neq 0\Leftrightarrow$$ $$\left | x \right |-2\left | x \right |^{2} \neq 0\Leftrightarrow$$ $$\left | x \right |(1-2\left | x \right |)\neq 0\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 0\\ x\neq 0,5\\ x\neq -0,5\end{matrix}\right.$$.
При $$x>0$$: $$y=\frac{2x-1}{x(1-2x)}=-\frac{1}{x}$$ (выдерена красным)
При $$x<0$$: $$y=\frac{-2x-1}{-x-2x^{2}}=\frac{1}{x}$$(выделена красным)
Итоговый график с учетом ОДЗ:
Найдем k: $$y=kx$$ проходит через (-0,5 ; -2): $$-2=-0,5*k\Rightarrow k=4$$(зеленая) и через (0,5; -2): $$-2=0,5k\Rightarrow k=-4$$(красная). При k=0 (черная) тоже не имеет пересечений
Задание 22
Отрезки $$AB$$ и $$CD$$ являются хордами окружности. Найдите длину хорды $$CD$$, если $$AB=24$$, а расстояния от центра окружности до хорд $$AB$$ и $$CD$$ равны соответственно $$16$$ и $$12$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Высоты $$BB_{1}$$ и $$CC_{1}$$ остроугольного треугольника $$ABC$$ пересекаются в точке $$E$$. Докажите, что углы $$BB_{1}C_{1}$$ и $$BCC_{1}$$равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


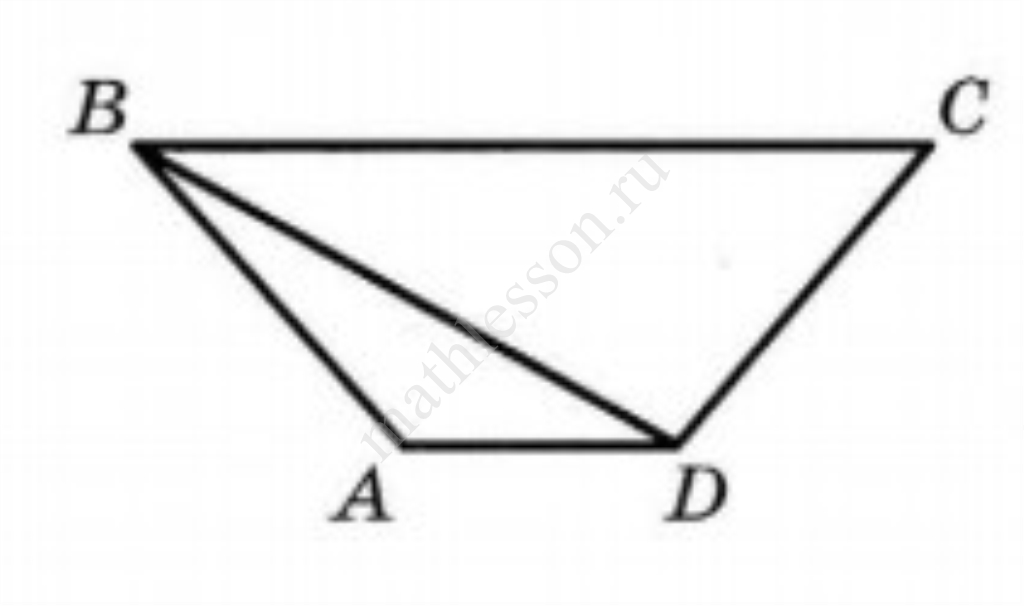
Задание 24
В выпуклом четырёхугольнике $$ABCD$$ диагонали пересекаются в точке $$O$$. Точка $$F$$ принадлежит отрезку $$AC$$. Известно, что $$BO=19$$, $$DO=16$$, $$AC=24$$. Найдите $$AF$$, если площадь треугольника $$FCD$$ в три раза меньше площади четырёхугольника $$ABCD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!