ОГЭ 2021. Вариант 3. Ященко 36 вариантов ФИПИ школе.
Решаем 3 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 3 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
Квартиры
На рисунке изображён план двухкомнатной квартиры с панорамной лоджией в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна (и остекления лоджии), а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Самое большое по площади помещение – гостиная. В спальне, гостиной и кухне есть двери и окна, выходящие на лоджию, но в кухне окно шире, чем в других комнатах. Остекление лоджии со стороны кухни закруглено. В квартире есть два помещения, в которых нет окон – это прихожая и санузел.
1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
| Помещение | спальня | гостиная | прихожая | лоджия | кухня |
| Цифры |
2. Найдите радиус закругления остекления лоджии со стороны кухни. Ответ дайте в сантиметрах.
3. Плитка для пола размером 10 см х 20 см продаётся в упаковках по 6 штук. Сколько упаковок плитки необходимо купить, чтобы выложить пол санузла?
4. Сколько процентов составляет площадь гостиной от площади прихожей?
5. Найдите площадь лоджии. Считайте $$\pi$$ равным 3,14. Ответ округлите до десятых квадратного метра.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Рассмотрим данные из условия:
- Вход в квартиру находится в прихожей. (2)
- Самое большое по площади помещение – гостиная. (1)
- … в кухне окно шире, чем в других комнатах. (4)
- Остекление лоджии со стороны кухни закруглено. (5)
- В спальне, гостиной и кухне есть двери и окна, выходящие на лоджию … (6)
2) По рисунку видим, что радиус равен 4 клетки. Одна клетка равна 0,4 м, тогда 4 клетки это: 4·0,4 = 1,6 м. Переведём в см: 1,6·100 = 160 см
3) Найдём площадь (прямоугольник) комнаты в клетках: 4·7 = 28 клеток. Одна клетка равна 0,4 м = 40 см, выразим площадь в см2: 28·40·40 = 44800 см2 .
Площадь одной плитки для пола равна: 10·20 = 200 см2. Найдём сколько плиток нам понадобится на весь пол: 44800/200 = 224 плитки.
В одной упаковке 6 штук, значит нам надо: 224/6 ≈ 37,333… Такое количество нам не продадут, значит покупаем 38 упаковок.
4) Площадь гостиной (1) это площадь прямоугольника: S1 = 15·9 = 135 клеток. Прихожая (2) это два прямоугольника, её площадь: S2 = 12·4 + 4·3 = 60 клеток. Найдём сколько процентов площадь гостиной (1) составляет от площади прихожей (2) (за 100% принимается то, с чем сравнивают):
Тогда : $$x=\frac{135*100}{60}=225$$.
5) Площадь лоджии состоит из прямоугольника и четверти (т.к. угол сегмента прямой) круга ($\frac{1}{4}$) c радиусом 4 клетки:
$$21\cdot 4+\frac{1}{4}\pi 4^{2}=84+4\cdot 3,14=96,56$$
Площадь одной клетки со стороной 0,4 м равна: 0,4·0,4 = 0,16 м2. Тогда площадь лоджии в метрах, округлённая до десятых равна:
$$96,56\cdot 0,16=14,4496\approx 15,4$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Сколько целых чисел расположено между числами $$\sqrt{13}$$ и $$\sqrt{130}$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$(x - 1)(-x - 4) = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
При подготовке к экзамену Олег выучил $$40$$ билетов, а $$10$$ билетов не выучил. Найдите вероятность того, что ему попадётся выученный билет.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


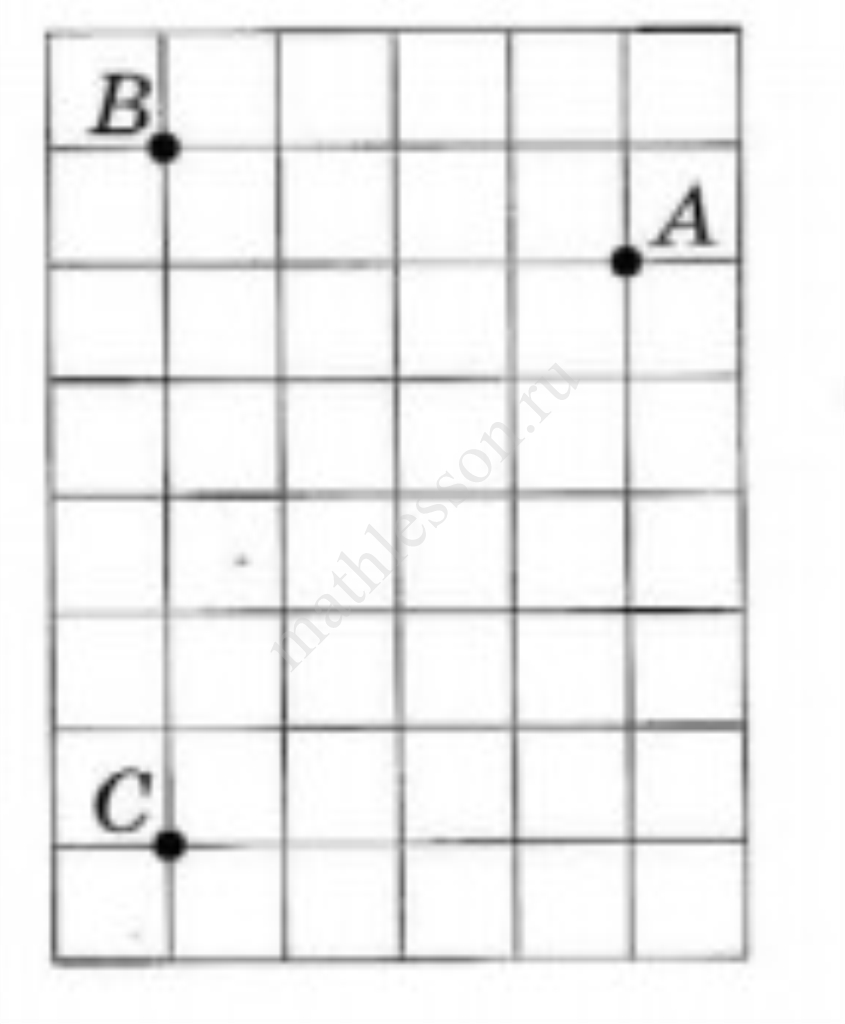
Общий вид линейной функции $$y=kx+b$$. При этом если $$k>0$$, то концы прямой находятся в первой и третьей координатных четвертях, если $$k<0$$, то во второй и четвертой. Если $$b>0$$, то прямая пересекает ось Оу над осью Ох, если $$b<0$$, то под осью. Получим:
- $$y=-\frac{2}{3}+4$$ - 2
- $$y=\frac{2}{3}x-4$$ - 1
- $$y=\frac{2}{3}x+4$$ - 3
Задание 12
Закон Кулона можно записать в виде $$F = k \frac{q_1 q_2}{r^2}$$, где $$F$$ — сила взаимодействия зарядов (в ньютонах), $$q_1$$ и $$q_2$$ — величины зарядов (в кулонах), $$k$$ — коэффициент пропорциональности (в Н·м²/Кл²), а $$r$$ — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда $$q_1$$ (в кулонах), если $$k = 9 \cdot 10^9$$ Н·м²/Кл², $$q_2 = 0,002$$ Кл, $$r = 2000$$ м, $$F = 0,00135$$ Н.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Найдите решение системы неравенств:
$$\left\{\begin{aligned}x + 0,6 &\le 0\\x - 1 &\ge -4\end{aligned}\right.$$
1) $$( -\infty;\ -3 ]$$
2) $$[ -0,6;\ +\infty )$$
3) $$( -\infty;\ -3 ];\ [ -0,6;\ +\infty )$$
4) $$[ -3;\ -0,6 ]$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
При проведении химического опыта реагент равномерно охлаждали на $$7,5^\circ\text{С}$$ в минуту. Найдите температуру реагента (в градусах Цельсия) спустя $$6$$ минут после начала проведения опыта, если начальная температура составляла $$-8,7^\circ\text{С}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какое из следующих утверждений верно?
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
- Средняя линия трапеции равна сумме её оснований.
В ответ запишите номер выбранного утверждения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- верно, по признаку подобия треугольников;
- неверно, они могут и не пересекаться;
- неверно, средняя линия трапеции равна полусумме её оснований;
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Заметим, что $$x^2 + 6x + 9 = (x + 3)^2.$$ Тогда: $$(x - 1)(x + 3)^2 = 5(x + 3).$$ Вынесем общий множитель: $$(x + 3)\bigl((x - 1)(x + 3) - 5\bigr) = 0.$$ Отсюда либо $$x + 3 = 0,$$ либо $$(x - 1)(x + 3) - 5 = 0.$$
2) Первый корень: $$x = -3.$$
3) Решаем второе уравнение: $$(x - 1)(x + 3) - 5 = 0,$$ $$x^2 + 2x - 3 - 5 = 0,$$ $$x^2 + 2x - 8 = 0.$$ Дискриминант: $$D = 2^2 - 4\cdot 1\cdot(-8) = 4 + 32 = 36.$$ Корни: $$x_{1,2} = \frac{-2 \pm \sqrt{36}}{2} = \frac{-2 \pm 6}{2},$$ $$x_1 = 2,\qquad x_2 = -4.$$
Задание 21
Имеются два сосуда, содержащие $$12$$ кг и $$8$$ кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий $$65 \%$$ кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать $$60 \%$$ кислоты. Сколько процентов кислоты содержится во втором растворе?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


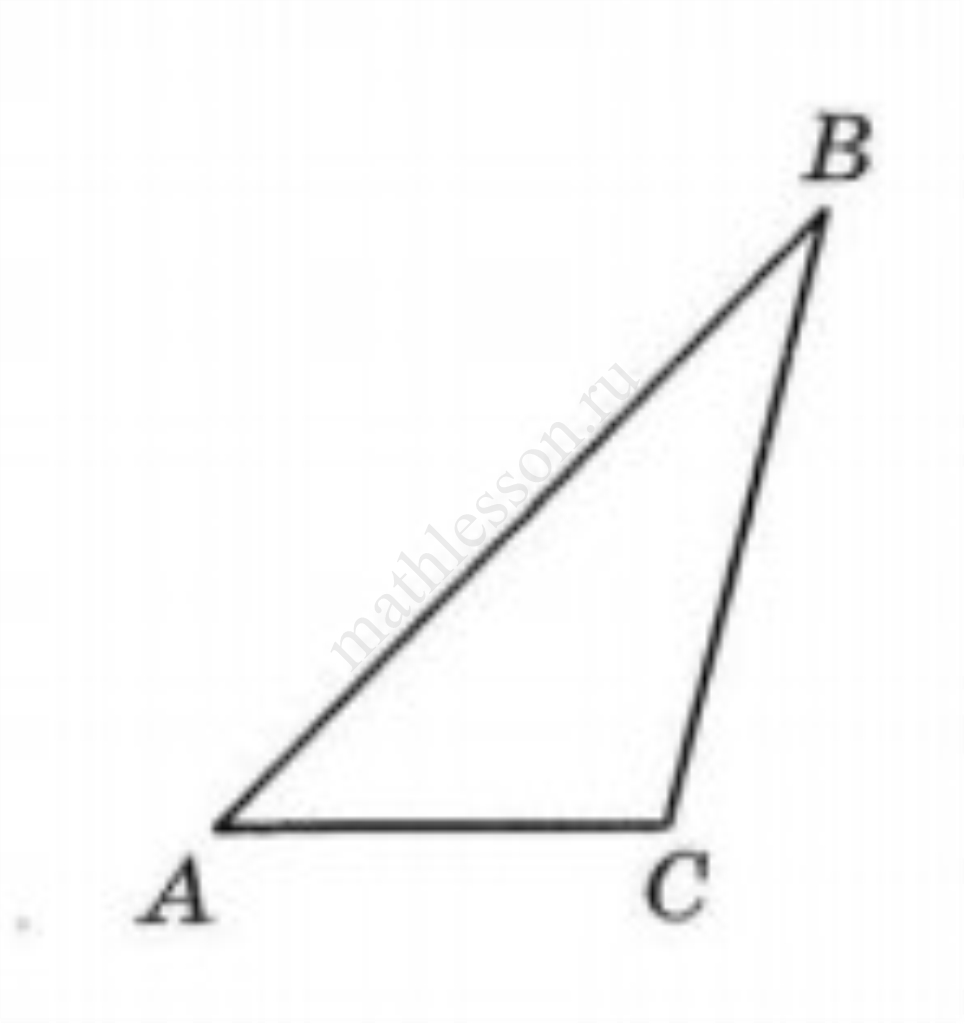
Задание 22
Прямая пересекает стороны $$AB$$ и $$BC$$ треугольника $$ABC$$ в точках $$K$$ и $$N$$ соответственно. Известно, что $$AB=CN=16$$, $$BC=20$$, $$AC=28$$, $$AK=11$$. Найдите длину отрезка $$KN$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!