ОГЭ 2024. Вариант 10 Ященко 36 вариантов ФИПИ школе.
Решаем 10 вариант ОГЭ Ященко 2024 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 10 варианта (всех заданий) Ященко 2024 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
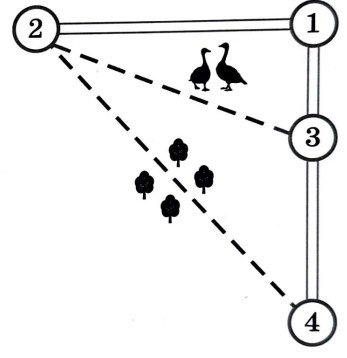
План местности
Аня летом отдыхает у дедушки и бабушки в деревне Николаевка. Аня с дедушкой собираются съездить на машине на железнодорожную станцию Путятино. Из Николаевки в Путятино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе - через посёлок Ковылкино до деревни Лесная, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Путятино. Есть и третий маршрут: в Ковылкино можно свернуть на прямую грунтовую дорогу, которая идёт мимо птицефабрики прямо в Путятино. По шоссе Аня с дедушкой едут со скоростью 72 км/ч, а по грунтовым дорогам - 50 км/ч. Расстояние по шоссе от Николаевки до Ковылкино равно 36 км, от Николаевки до Лесной - 60 км, а от Лесной до Путятино - 45 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр.
| Насел. пункты | д. Лесная | п. Ковылкино | д. Николаевка | ст. Путятино |
| Цифры |
2. На сколько процентов скорость, с которой едут Аня с дедушкой по шоссе, больше их скорости по грунтовой дороге?
3. Найдите расстояние от деревни Николаевка до станции Путятино по прямой. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Аня с дедушкой, если поедут на по прямой грунтовой дороге от Николаевки до Путятино?
5. На грунтовых дорогах машина дедушки расходует 9,2 литра бензина на 100 Известно, что на путь из Николаевки до Путятино через Ковылкино мим птицефабрики и на путь через деревню Лесная ей необходим одив и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе? Ответ:
Задание 6
Найдите значение выражения: $$\frac{1}{\frac{1}{72}-\frac{1}{99}}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$(5x + 2)( -x - 4) = 0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Врач прописал больному капли по следующей схеме: в первый день $$10$$ капель, а в каждый следующий день — на $$10$$ капель больше, чем в предыдущий, до тех пор, пока дневная доза не достигнет $$80$$ капель. Такую дневную дозу ($$80$$ капель) больной ежедневно принимает три дня, а затем уменьшает приём на $$10$$ капель в день до последнего дня, когда больной принимает последние $$10$$ капель. Сколько пузырьков лекарства нужно купить на весь курс, если в каждом пузырьке $$5$$ мл лекарства, то есть $$150$$ капель?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Решите систему уравнений: $$\left\{\begin{aligned} 3x^2 + 2y^2 = 50 \\ 12x^2 + 8y^2 = 50x \end{aligned}\right.$$
1) Во втором уравнении левая часть равна четырёхкратной левой части первого: $$12x^2 + 8y^2 = 4(3x^2 + 2y^2).$$ Умножим первое уравнение на $$4$$: $$12x^2 + 8y^2 = 200.$$ Согласно второму уравнению: $$12x^2 + 8y^2 = 50x.$$ Приравниваем: $$200 = 50x \;\Rightarrow\; x = 4.$$
2) Подставим $$x = 4$$ в первое уравнение: $$3\cdot 4^2 + 2y^2 = 50 \;\Rightarrow\; 48 + 2y^2 = 50 \;\Rightarrow\; 2y^2 = 2 \;\Rightarrow\; y^2 = 1,$$ откуда $$y = 1$$ или $$y = -1.$$ Решения: $$(4;1),\ (4;-1).$$