ОГЭ 2021. Вариант 16 Ященко 36 вариантов ФИПИ школе.
Решаем 16 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 16 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
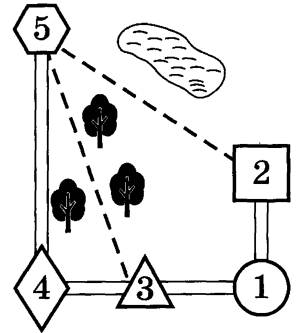
План местности
Юля летом отдыхает у дедушки и бабушки в деревне Царёво. Юля с дедушкой собираются съездить на машине на железнодорожную станцию Таировка. Из Царёво в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через посёлок Демидово. Из Царёво в Таировку можно проехать через посёлок Демидово и не заезжая в Ключи, но тогда первую часть пути надо будет ехать по прямой лесной дороге. Есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево и там, повернув направо, по шоссе добраться до Таировки.
По шоссе Юля с дедушкой едут со скоростью 60 км/ч, а по лесной и грунтовой дорогам 45 км/ч. Расстояние по шоссе от Царёво до Ключей равно 72 км, от Таировки до Ключей — 60 км, от Таировки до Демидово — 30 км, а от Таировки до Федяево — 27 км.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр. Насел. пункты п. Демидово д. Ключи ст. Таировка с. Федяево д. Царёво Цифры
Задание 2.
На сколько процентов скорость, с которой едут Юля с дедушкой по грунтовой дороге, меньше их скорости по шоссе?
Задание 3.
Сколько минут затратят на дорогу Юля с дедушкой, если поедут на станцию через Ключи?
Задание 4.
Найдите расстояние от д. Царёво до п. Демидово по лесной дороге, Ответ дайте в километрах.
Задание 5.
Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Юля с дедушкой, если поедут этим маршрутом.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1.
С учетом того, что из Царёво в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через посёлок Демидово, получим, что:
Кроме того, есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево. Получаем, 2 – Федяево.
Задание 2.
Скорость движения по тропинке 45 км/ч, а по шоссе 60 км/ч. Разница в скоростях составляет 15 км/ч. Сравнивают со скоростью по шоссе:
Тогда: $$x=\frac{15\cdot 100}{60}=25%$$ - разница в процентах
Задание 3.
Пусть на станцию через Ключи равен 72+60=132 км. По шоссе скорость 60 км/ч, тогда время движения в часах: $$\frac{132}{60}$$ часа. Так как в 1 часе 60 минут, то время в минутах: $$\frac{132}{60}\cdot 60=132$$ минуты
Задание 4.
Расстояние от д. Царёво до п. Демидово по лесной дороге – это гипотенуза прямоугольного треугольника с катетами 72 и 60-30=30 км. По теореме Пифагора находим расстояние: $$\sqrt{72^{2}+30^{2}}=78$$ км.
Задание 5.
- По шоссе время уже найдено: 132 минуты
- Время через Демидово (аналогично заданию 3): $$\frac{78}{45}\cdot 60=134$$ минуты.
- По прямой грунтовой дороге: $$\frac{\sqrt{60^{2}+(72-27)^{2}}}{45}\cdot 60+\frac{27}{60}\cdot 60=127$$ минут - наименьшее время
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Какое из следующих чисел заключено между числами $$\frac{19}{8}$$ и $$\frac{17}{7}$$?
1) $$2,4$$
2) $$2,5$$
3) $$2,6$$
4) $$2,7$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$(x - 6)( -5x - 9 ) = 0$$. Если уравнение имеет более одного корня, в ответ запишите меньший из них.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
В группе туристов $$20$$ человек. С помощью жребия они выбирают трёх человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист К., входящий в состав группы, пойдёт в магазин?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Теорему синусов можно записать в виде $$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}$$, где $$a$$ и $$b$$ — две стороны треугольника, а $$\alpha$$ и $$\beta$$ — углы треугольника, лежащие против этих сторон соответственно. Пользуясь этой формулой, найдите величину $$\sin \alpha$$, если $$a = 21$$, $$b = 5$$, $$\sin \beta = \frac{1}{6}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение неравенства: $$x^2 - 25 > 0$$
1) $$( -\infty;\ -5 ) \cup ( 5;\ +\infty )$$
2) $$( -5;\ 5 )$$
3) нет решений
4) $$( -\infty;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
К концу $$2011$$ года в городе проживало $$102\ 300$$ человек. Каждый год число жителей города возрастало на одну и ту же величину. В конце $$2018$$ года в городе проживало $$114\ 340$$ человек. Какова была численность населения этого города к концу $$2016$$ года?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Точки $$M$$ и $$N$$ являются серединами сторон $$AB$$ и $$BC$$ треугольника $$ABC$$, сторона $$AB = 57$$, сторона $$BC = 74$$, сторона $$AC = 48$$. Найдите $$MN$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Угол $$A$$ трапеции $$ABCD$$ с основаниями $$AD$$ и $$BC$$, вписанной в окружность, равен $$83^\circ$$. Найдите угол $$B$$ этой трапеции. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
В ромбе $$ABCD$$ угол $$ABC$$ равен $$58^\circ$$. Найдите угол $$ACD$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Сумма углов равнобедренного треугольника равна $$180^{\circ}$$ градусам.
- Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
- В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Найдите значение выражения: $$31a - 4b + 55$$, если $$\frac{a - 4b + 7}{4a - b + 7} = 8$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


По условию $$\frac{a-4b+7}{4a-b+7}=8$$.
Умножим обе части равенства на $$4a-b+7$$: $$a-4b+7=8(4a-b+7).$$
Раскроем скобки и перенесём всё в одну часть: $$0=32a-8b+56-(a-4b+7)=31a-4b+49,$$ откуда $$31a-4b+49=0.$$ Тогда $$31a-4b=-49.$$
Прибавим к обеим частям равенства $$55$$: $$31a-4b+55=-49+55=6.$$ Следовательно, значение выражения $$31a-4b+55$$ равно $$6$$.
Задание 21
Семь одинаковых рубашек дешевле куртки на $$9 \%$$. На сколько процентов десять таких же рубашек дороже куртки?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = \frac{(x^2 + 4)(x + 1)}{-1 - x}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Биссектриса угла $$A$$ параллелограмма $$ABCD$$ пересекает сторону $$BC$$ в точке $$K$$. Найдите периметр параллелограмма, если $$BK=8$$, $$CK=13$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Окружности с центрами в точках $$P$$ и $$Q$$ пересекаются в точках $$K$$ и $$L$$, причём точки $$P$$ и $$Q$$ лежат по одну сторону от прямой $$KL$$. Докажите, что $$PQ\perp KL$$ .
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 25
В треугольнике $$ABC$$ биссектриса $$BE$$ и медиана $$AD$$ перпендикулярны и имеют одинаковую длину, равную $$12$$. Найдите стороны треугольника $$ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!