ОГЭ 2021. Вариант 26 Ященко 36 вариантов ФИПИ школе.
Решаем 26 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 26 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
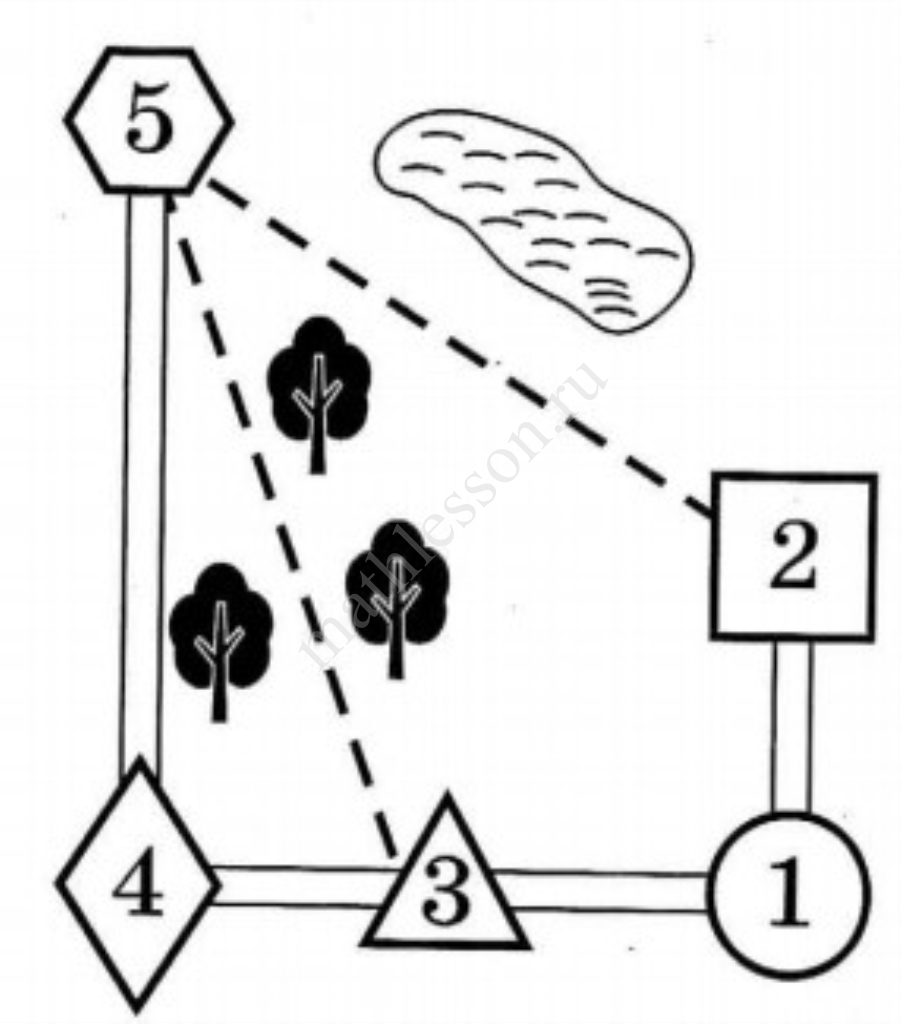
План местности
Аня летом отдыхает у дедушки и бабушки в деревне Борисовке. Аня с дедушкой собираются съездить на велосипедах в село Красное на железнодорожную станцию. Из Борисовки в Красное можно проехать по шоссе до деревни Емелино, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Красное через посёлок Лошкари. Из Борисовки в Красное можно проехать через посёлок Лошкари и не заезжая в Емелино, но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо озера до деревни Устье и там, повернув направо, по шоссе добраться до Красного.
По шоссе Аня с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Борисовки до Емелино равно 15 км, от Красного до Емелино - 24 км, от Красного до Лошкарей - 16 км, а от Красного до Устья - 8 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр.
| Насел. пункты | д. Борисовка | д. Устье | п. Лошкари | с. Красное | д. Емелино |
| Цифры |
2. Сколько километров проедут Аня с дедушкой, если они поедут на станцию по шоссе через Емелино?
3. Сколько минут затратят на дорогу Аня с дедушкой, если поедут на станцию через Емелино?
4. Найдите расстояние от д. Борисовка до п. Устье по прямой тропинке. Ответ дайте в километрах.
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Аня с дедушкой, если поедут этим маршрутом.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$(\sqrt{45} - \sqrt{5}) \cdot \sqrt{5}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите уравнение: $$x^2 + 4x = 21$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На семинар приехали $$7$$ учёных из Австрии, $$8$$ из России и $$10$$ из Швеции. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Кинетическая энергия тела вычисляется по формуле $$E = \frac{mv^2}{2}$$, где $$m$$ — масса тела (в килограммах), а $$v$$ — его скорость (в метрах в секунду). Пользуясь этой формулой, найдите $$E$$ (в джоулях), если $$v = 5$$ м/с и $$m = 12$$ кг.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите неравенство, которое не имеет решений:
1) $$x^2 - 2x - 65 0$$
2) $$x^2 - 2x - 65 > 0$$
3) $$x^2 - 2x + 65 0$$
4) $$x^2 - 2x + 65 > 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
В $$7:00$$ часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В $$22:00$$ того же дня часы отставали на час. На сколько минут отставали часы спустя $$17$$ часов после того, как они сломались?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
Синус острого угла $$A$$ треугольника $$ABC$$ равен $$\frac{\sqrt{51}}{10}$$. Найдите $$\cos A$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны?
- Смежные углы всегда равны.
- Площадь квадрата равна произведению двух его смежных сторон.
- Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Разложим числа на простые множители:
$$100=2^2\cdot 5^2,\quad 4=2^2$$
Тогда $$100^n=(2^2\cdot 5^2)^n=2^{2n}\cdot 5^{2n}$$, а $$4^{n-2}=(2^2)^{n-2}=2^{2n-4}$$.
2) Подставим в дробь: $$\frac{100^n}{5^{2n-3}\cdot 4^{n-2}}=\frac{2^{2n}\cdot 5^{2n}}{5^{2n-3}\cdot 2^{2n-4}}$$
3) Сократим степени: $$\frac{2^{2n}\cdot 5^{2n}}{5^{2n-3}\cdot 2^{2n-4}} =2^{2n-(2n-4)}\cdot 5^{2n-(2n-3)}=2^4\cdot 5^3$$
4) Вычислим: $$2^4\cdot 5^3=16\cdot 125=2000$$
Задание 21
Первые $$500$$ км автомобиль ехал со скоростью $$100$$ км/ч, следующие $$100$$ км — со скоростью $$50$$ км/ч, а затем $$165$$ км — со скоростью $$55$$ км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Постройте график функции $$y = |x|x + 3|x| - 5x$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно $$14$$, а одна из диагоналей ромба равна $$56$$. Найдите углы ромба.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
На средней линии трапеции $$ABCD$$ с основаниями $$AD$$ и $$BC$$ выбрали произвольную точку $$K$$. Докажите, что сумма площадей треугольников $$BKC$$ и $$AKD$$ равна половине площади трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!