ОГЭ 2023. Вариант 18 Ященко 36 вариантов ФИПИ школе.
Решаем 18 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 18 варианта (всех заданий) Ященко 2023 ФИПИ 36 вариантов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Между какими целыми числами заключено число $$\frac{140}{17}$$?
1) $$5$$ и $$6$$
2) $$6$$ и $$7$$
3) $$7$$ и $$8$$
4) $$8$$ и $$9$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Найдите значение выражения $$\sqrt{\frac{1}{16} \cdot x^{10} \cdot y^2}$$ при $$x = 2$$, $$y = 3$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
В среднем из каждых $$50$$ поступивших в продажу аккумуляторов $$47$$ аккумуляторов заряжены. Найдите вероятность того, что выбранный в магазине наудачу аккумулятор не заряжен.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между знаками коэффициентов $$a$$ и $$c$$ и графиками функций.
Коэффициенты
А. $$a > 0$$; $$c < 0$$
Б. $$a > 0$$; $$c > 0$$
В. $$a < 0$$; $$c > 0$$
ГРАФИКИ
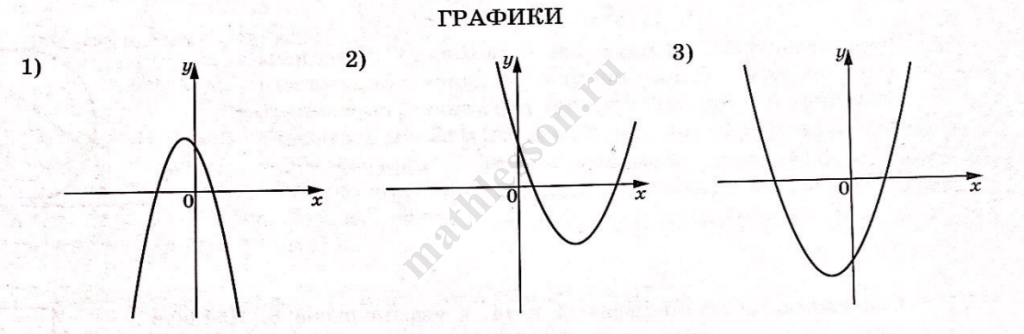
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле $$r = \frac{a + b - c}{2}$$, где $$a$$ и $$b$$ — катеты, а $$c$$ — гипотенуза. Пользуясь этой формулой, найдите $$c$$, если $$a = 12$$, $$b = 35$$ и $$r = 5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой $$16$$ мг. Каждые $$20$$ минут масса колонии увеличивается в $$3$$ раза. Найдите массу колонии микроорганизмов через $$60$$ минут после начала эксперимента. Ответ дайте в миллиграммах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Через точку $$A$$, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке $$K$$. Другая прямая пересекает окружность в точках $$B$$ и $$C$$, причём $$AB = 4$$, $$BC = 12$$. Найдите $$AK$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Основания трапеции равны $$4$$ и $$14$$, а высота равна $$8$$. Найдите среднюю линию этой трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Какие из следующих утверждений верны?
- Через заданную точку плоскости можно провести только одну прямую.
- Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около этого треугольника.
- Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Решите систему уравнений: $$ \left\{ \begin{aligned} (x - 4)(y - 7) = 0\\ \frac{y - 5}{x + y - 9} = 2 \end{aligned} \right. $$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Из первого уравнения получаем: $$(x-4)(y-7)=0 \Rightarrow x=4$$ или $$y=7.$$
1) Пусть $$x=4.$$ Подставим во второе уравнение: $$\dfrac{y-5}{4+y-9}=2 \;\Rightarrow\; \dfrac{y-5}{y-5}=2.$$ Если $$y\neq5,$$ то левая часть равна $$1,$$ получаем противоречие $$1=2.$$ Если $$y=5,$$ то знаменатель равен нулю, дробь не имеет смысла. Следовательно, при $$x=4$$ решений нет.
2) Пусть $$y=7.$$ Подставим во второе уравнение: $$\dfrac{7-5}{x+7-9}=2 \;\Rightarrow\; \dfrac{2}{x-2}=2.$$ Отсюда $$\dfrac{2}{x-2}=2 \;\Rightarrow\; \dfrac{1}{x-2}=1 \;\Rightarrow\; x-2=1 \;\Rightarrow\; x=3.$$ Проверим знаменатель: $$x+y-9=3+7-9=1\neq 0.$$ Значит, пара $$(3;7)$$ является решением системы.
Задание 20
Расстояние между пристанями $$A$$ и $$B$$ равно $$60$$ км. Из $$A$$ в $$B$$ по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт $$B$$, тотчас повернула обратно и возвратилась в $$A$$. К этому времени плот проплыл $$30$$ км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна $$5$$ км/ч. Ответ дайте в км/ч.
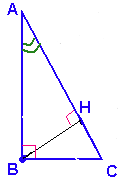
Задание 22
Точка $$H$$ является основанием высоты, проведённой из вершины прямого угла $$B$$ треугольника $$ABC$$ к гипотенузе $$AC$$. Найдите $$AB$$, если $$AH=9$$, $$AC=36$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
Биссектрисы углов $$A$$ и $$D$$ трапеции $$ABCD$$ пересекаются в точке $$M$$, лежащей на стороне $$BC$$. Докажите, что точка $$M$$ равноудалена от прямых $$AB$$, $$AD$$ и $$CD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 24
Четырёхугольник $$ABCD$$ со сторонами $$AB=12$$ и $$CD=30$$ вписан в окружность. Диагонали $$AC$$ и $$BD$$ пересекаются в точке $$K$$, причём $$\angle AKB=60^{\circ}$$. Найдите радиус окружности, описанной около этого четырёхугольника.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!