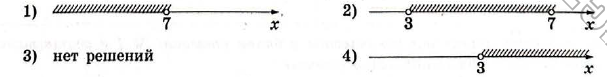ОГЭ 2026. Вариант 4 Ященко 36 вариантов ФИПИ школе.
Решаем 4 вариант ОГЭ Ященко 2026 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 4 варианта (всех заданий) Ященко 2026 ФИПИ 36 вариантов.
Рутуб
Ютуб
Задания:
Задание 1-5
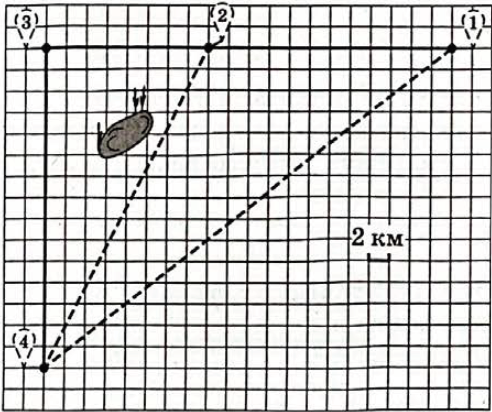
Маша летом отдыхает у дедушки в деревне Вешки. В субботу они собираются съездить на машине в село Белое. Из деревни Вешки в село Белое можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Орловка до деревни Заулки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Белое. Есть и третий маршрут: в деревне Орловка можно свернуть на прямую грунтовую дорогу в село Белое, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Маша с дедушкой едут со скоростью $$50$$ км/ч, а по грунтовой дороге — со скоростью $$40$$ км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна $$2$$ км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
| Насел. пункты | д. Заулки | д. Орловка | с. Белое |
| Цифры |
2. Найдите расстояние от деревни Орловка до села Белое по прямой. Ответ дайте в километрах.
3. Сколько минут затратят Маша с дедушкой на дорогу из деревни Вешки в село Белое, если поедут по шоссе до деревни Орловка, а потом свернут на прямую грунтовую дорогу, которая идет мимо пруда?
4. На сколько процентов расстояние от деревни Вешки до села Белое через деревню Заулки больше расстояния между этими пунктами по прямой?
5. В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в селе Игнатово и в деревнях Починки, Власово и Крынки.
| Наименование продукта | д. Вешки | с. Белое | д. Орловка | д. Заулки |
| Молоко (1 л) | 85 | 80 | 90 | 76 |
| Хлеб (1 батон) | 50 | 55 | 60 | 45 |
| Сыр «Сливочный» (1 кг) | 600 | 550 | 500 | 520 |
| Говядина (1 кг) | 830 | 750 | 780 | 800 |
| Картофель (1 кг) | 85 | 75 | 90 | 80 |
Маша с дедушкой хотят купить $$4$$ л молока, $$2$$ кг сыра «Сливочный» и $$4$$ кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
1) по прямолинейному шоссе через деревню Орловка до деревни Заулки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Белое - следовательно, $$3$$ - Заулки, $$2$$ - Орловка, $$4$$ - Белое, $$1$$ - Вешки
Тогда ответ: $$324$$
2) С учетом, что $$1$$ клетка по масштабу равна $$2$$ км, то расстояние (по первым буквам названия населенного пункта): ВО: $$24$$ км; ОЗ: $$16$$ км; ЗБ: $$30$$ км.
ОБ: $$\sqrt{16^2 + 30^2} = \sqrt{1156} = 34$$ км.
3) По шоссе $$24$$ км. Скорость движения по шоссе $$50$$ км/ч. По грунтовой дороге $$34$$ км, скорость движения по грунтовой дороге $$40$$ км/ч. Тогда время в минутах: $$(\frac{24}{50} + \frac{34}{40})\cdot 60 = 79,8$$ минут.
4) ВБ: $$\sqrt{40^2 + 30^2} = 50$$ км. ВКИ: $$24 + 16 + 30 = 70$$ км. Разность расстояний $$20$$ км. Составим пропорцию:
$$50$$ км - $$100\%$$
$$20$$ км - $$x\%$$
$$x = \frac{20 \cdot 100}{50} = 40\%$$
5) Распишем стоимость продуктового набора для каждого населенного пункта:
В: $$4 \cdot 85 + 2 \cdot 600 + 4 \cdot 85 = 1880$$
Б: $$4 \cdot 80 + 2 \cdot 550 + 4 \cdot 75 = 1720$$
О: $$4 \cdot 90 + 2 \cdot 500 + 4 \cdot 90 = 1720$$
З: $$4 \cdot 75 + 2 \cdot 520 + 4 \cdot 80 = 1660$$ - наименьшая стоимость.
Задание 7
Какое из чисел $$\frac{67}{14}$$, $$\frac{76}{14}$$, $$\frac{85}{14}$$ и $$\frac{93}{14}$$ принадлежит отрезку $$[5 ; 6]$$:
1) $$\frac{67}{14}$$
2) $$\frac{76}{14}$$
3) $$\frac{85}{14}$$
4) $$\frac{93}{14}$$
В ответе запишите номер выбранного числа.
$$\frac{67}{14} \approx 4,79$$, $$\frac{76}{14} \approx 5,43$$, $$\frac{85}{14} \approx 6,07$$, $$\frac{93}{14} \approx 6,64$$
По условию должно принадлежать отрезку $$[5; 6]$$
Подходит $$\frac{76}{14}$$ → номер $$3$$
Задание 8
Найдите значение выражения $$\frac{m^{15} \cdot (n^3)^6}{(m \cdot n)^{16}}$$ при $$m = 2$$ и $$n = \sqrt{7}$$.
$$\frac{m^{15} \cdot (n^3)^6}{(m \cdot n)^{16}} =$$ $$\frac{m^{15} \cdot n^{18}}{m^{16} \cdot n^{16}} = m^{-1} \cdot n^{2} = \frac{n^2}{m} = \frac{7}{2}=3,5$$
- Раскроем скобки в левой части уравнения:
$$8 + 3 \cdot 4 - 3 \cdot x = 2x + 7$$
$$8 + 12 - 3x = 2x + 7$$ - Сложим числа в левой части: $$20 - 3x = 2x + 7$$
- Перенесём все члены с $$x$$ в правую часть, а числовые члены — в левую:
$$20 - 7 = 2x + 3x$$
$$13 = 5x$$ - Разделим обе части уравнения на $$5$$, чтобы найти $$x$$:
$$x = \frac{13}{5}$$
$$x = 2{,}6$$
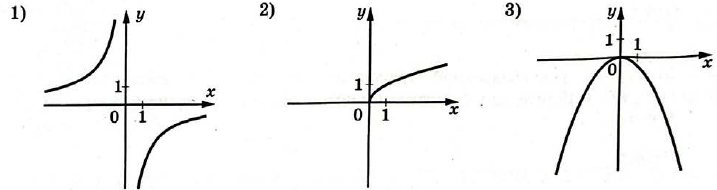
Задание 11
1) гипербола во $$2$$-й и $$4$$-й четвертях → В
2) ветвь параболы в первой четверти → Б
3) парабола с вершиной в $$(0; 0)$$ → А
Тогда правильный ответ: $$321$$
Задание 12
Теорему синусов можно записать в виде $$\frac{a}{\sin\alpha} = \frac{b}{\sin\beta}$$ где $$a$$ и $$b$$ — две стороны треугольника, а $$\alpha$$ и $$\beta$$ — углы треугольника, лежащие против них соответственно. Пользуясь этой формулой, найдите величину $$\sin\alpha$$, если $$a = 6$$, $$b = 5$$, $$\sin\beta = 0,2$$.
Подставим известные значения в формулу:
$$\frac{6}{\sin\alpha} = \frac{5}{0,2}$$
$$\frac{6}{\sin\alpha} = 25$$
$$\sin\alpha = \frac{6}{25} = 0,24$$
Задание 14
Каучуковый мячик с силой бросили на асфальт. Отскочив, мячик подпрыгнул на $$4,8$$ м, а при каждом следующем прыжке он поднимался на высоту в три раза меньше предыдущей. При каком по счёту прыжке мячик первый раз не достигнет высоты $$15$$ см?
$$4,8$$ м = $$480$$ см
Высоты: $$480$$, $$160$$, $$\frac{160}{3}$$, $$\frac{160}{9}=17\frac{7}{9}$$, $$\frac{160}{27}=5\frac{25}{27}$$ см
На $$5$$-м прыжке высота $$5\frac{25}{27} 15$$.
Задание 16
В треугольнике $$ABC$$ известно, что $$AC = 20$$, $$BC = 15$$, угол $$C$$ равен $$90^\circ$$. Найдите радиус описанной около этого треугольника окружности.
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы
Гипотенуза $$AB = \sqrt{AC^2 + BC^2} = \sqrt{400 + 225} = \sqrt{625} = 25$$
$$R = \frac{25}{2} = 12,5$$
Задание 17
Диагональ равнобедренной трапеции образует с её основанием угол $$45^\circ$$. Найдите длину высоты трапеции, если её основания равны $$4$$ и $$9$$.
Пусть $$BF$$ и $$CE$$ - высоты. Тогда $$BCEF$$ - прямоугольник и $$BC = FE = 4$$
Треугольники $$ABF$$ и $$CED$$ - равны по катету и гипотенузе, тогда $$AF = \frac{AD-BC}{2} = 2,5$$
$$\angle CAE = 45^\circ$$, то есть треугольник $$AEC$$ - прямоугольный и равнобедренный, тогда $$CE = AE = 2,5 + 4 = 6,5$$
Задание 19
Какие из следующих утверждений являются истинными высказываниями?
- Диагонали ромба точкой пересечения делятся пополам.
- Треугольник со сторонами $$1,2,4$$ существует.
- Через точка, не лежащую на данной прямой, можно провести прямую, параллельную данной.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
- Верно - и пересекаются под прямым углом.
- Неверно - сумма длин двух любых сторон в треугольнике всегда больше длины третьей стороны. А тут $$4 > 1 + 2$$
- Верно - притом только одну.
Задание 20
Решите неравенство $$-\frac{30}{x^2 - 7x - 30} \leq 0$$.
ОДЗ: $$x^{2} - 7x- 30\neq 0$$
$$\left\{\begin{matrix}x_{1}+x_{2}\neq 7\\x_{1}\cdot x_{2}\neq-30\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}\neq-3\\x_{2}\neq 10\end{matrix}\right.$$
$$-\frac{30}{x^2 - 7x - 30} \leq 0$$$$\Leftrightarrow$$ $$(x+3)(x-10)>0$$
Начертим координатную прямую и отметим значения $$x$$ , при которых знаменатель равен нулю (точки пустые согласно ОДЗ), расставим знаки, которые принимает выражение $$(x+3)(x-10)$$ на полученных промежутках:
Выберем промежутки, на которых выражение $$(x+3)(x-10)$$ принимает положительные значения: $$(-\infty; -3) \cup (10; +\infty)$$
Задание 21
Первый рабочий за час делает на $$6$$ деталей больше, чем второй, и выполняет заказ, состоящий из $$80$$ деталей, на $$3$$ часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
Пусть $$x$$ деталей в час - производительность первого, тогда $$x - 6$$ - второго. Тогда время выполнения заказа на $$80$$ деталей для первого $$t_1 = \frac{80}{x}$$ часов, для второго $$t_2 = \frac{80}{x - 6}$$. Получим:
$$\frac{80}{x - 6} - \frac{80}{x} = 3$$
$$80\left(\frac{1}{x - 6} - \frac{1}{x}\right) = 3$$
$$80 \cdot \frac{6}{x(x - 6)} = 3$$
$$480 = 3x(x - 6)$$
$$x^2 - 6x - 160 = 0$$
$$D = 36 + 640 = 676$$
$$x = \frac{6 + 24}{2} = 15$$ деталей в час
$$x = \frac{6 - 24}{2} = -9$$ - не может быть, так как $$x > 0 $$ исходя из условия задачи.
Задание 22
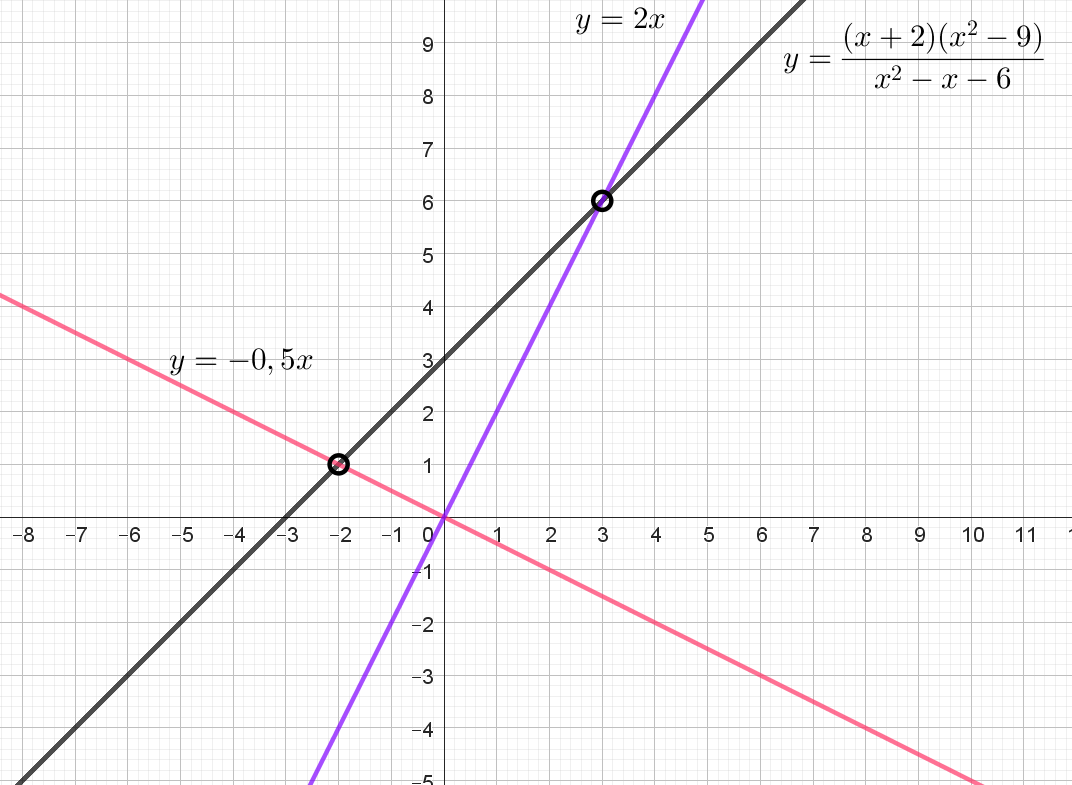
Постройте график функции $$y = \frac{(x+2)(x^2-9)}{x^2-x-6}$$
Определите, при каких значениях $$k$$ прямая $$y=kx$$ не имеет с графиком общих точек.
Разложим знаменатель на множители: $$x^2 - x - 6 = (x - 3)(x + 2)$$. Учтем, что $$x^2 - 9 = (x - 3)( x+ 3)$$
$$y = \frac{(x+2)(x-3)(x+3)}{(x-3)(x+2)} = x + 3$$ при $$x \neq -2; 3$$, так как знаменатель не может равнять нулю.
То есть графиком функции будет прямая $$y = x + 3$$, с учетом, что $$x \neq -2; y \neq -2+3 =1$$ и $$x \neq 3; y \neq 3 + 3 = 6$$
Пустые точки на графике: $$(-2; 1)$$, $$(3; 6)$$. На рисунке итоговая прямая выделена черным цветом.
Прямая $$y = kx$$ не имеет общих точек при:
Проходит через $$(-2; 1)$$ - выделена красным цветом. Подставим координаты данной точки в уравнение прямой: $$1 = k \cdot (-2) \Leftrightarrow k = -0,5$$
Проходит через $$(3; 6)$$ - выделена синим цветом. Подставим координаты данной точки в уравнение прямой: $$6 = k \cdot 3 \Leftrightarrow k = 2$$
Задание 23
Катет и гипотенуза прямоугольного треугольника равны $$25$$ и $$65$$. Найдите высоту, проведённую к гипотенузе.
По т. Пифагора второй катет: $$\sqrt{65^2 - 25^2} = \sqrt{4225 - 625} = \sqrt{3600} = 60$$
Найдем площадь, как половину произведения длин катетов: $$S = \frac{1}{2} \cdot 25 \cdot 60 = 750$$
С другой стороны, площадь можно вычислить, как половину произведения длин гипотенузы и высоты. Отсюда длина высоты: $$h = \frac{2S}{c} = \frac{1500}{65} = \frac{750}{13}$$
Задание 24
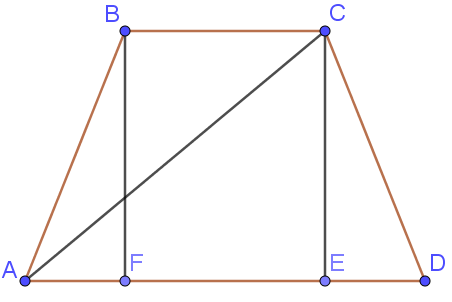
Точка $$K$$ — середина боковой стороны $$CD$$ трапеции $$ABCD$$, а $$AK = BK$$. Докажите, что трапеция $$ABCD$$ прямоугольная.
1) Пусть $$KH$$ - высота в треугольнике $$ABK$$, Тогда $$KH \perp AB$$.
2) Так как $$BK = AK$$, то треугольник $$ABK$$ - равнобедренный, тогда $$KH$$ - медиана. То есть $$H$$ - середина $$AB$$.
3) Тогда $$KH$$ - средняя линия трапеции $$ABCD$$, и $$KH \parallel AD \parallel BC$$.
4) Следовательно, $$BC\perp AB$$ и $$AD\perp AB$$, то есть трапеция - прямоугольная.
Задание 25
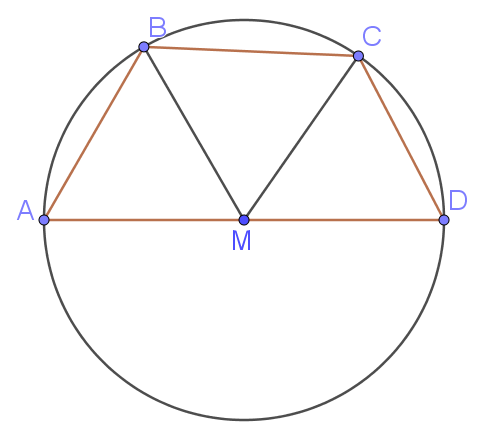
Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$BC$$, если $$AD = 12$$, а углы $$C$$ и $$D$$ четырёхугольника равны соответственно $$102^\circ$$ и $$72^\circ$$.
1) $$MA = MB = MC = MD$$, следовательно, около $$ABCD$$ можно описать окружность с центром $$M$$. Точка $$M$$ — середина $$AD$$, значит, $$AD$$ — диаметр этой окружности. Тогда $$AD = 12$$, откуда $$MA = MB = MC = MD = 6$$.
2) У вписанного четырёхугольника сумма противоположных углов равна $$180^\circ$$. Поэтому: $$\angle A = 180^\circ - \angle C = 180^\circ - 102^\circ = 78^\circ,$$ $$\angle B = 180^\circ - \angle D = 180^\circ - 72^\circ = 108^\circ.$$
3) Треугольник $$AMB$$ равнобедренный, так как $$MA = MB$$. Тогда $$\angle MAB = \angle ABM.$$ Но точка $$M$$ лежит на прямой $$AD$$, поэтому $$\angle MAB = \angle A = 78^\circ$$, значит, $$\angle ABM = 78^\circ.$$ Следовательно, $$\angle MBC = \angle B - \angle ABM = 108^\circ - 78^\circ = 30^\circ.$$
4) Треугольник $$BMC$$ тоже равнобедренный, так как $$MB = MC$$, значит $$\angle MBC = \angle BCM = 30^\circ.$$ Тогда $$\angle BMC = 180^\circ - 2\cdot 30^\circ = 120^\circ.$$
5) По теореме косинусов в треугольнике $$BMC$$: $$BC^2 = BM^2 + MC^2 - 2\cdot BM \cdot MC \cdot \cos \angle BMC.$$ Подставляем $$BM = MC = 6$$ и $$\cos 120^\circ = -\dfrac{1}{2}$$: $$BC^2 = 6^2 + 6^2 - 2\cdot 6\cdot 6 \cdot \left(-\frac{1}{2}\right) = 36 + 36 + 36 = 108,$$ $$BC = \sqrt{108} = 6\sqrt{3}$$
Ответ: $$BC = 6\sqrt{3}$$.