Квадратные неравенства
Задание 3893
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3486
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Решим уравнение $$x^{2}-2x-3=0$$
$$\left\{\begin{matrix}x_{1} +x_{2}=2& & \\x_{1}*x_{2}=-3 & &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x_{1}=3 & & \\x_{2}=-1 & &\end{matrix}\right.$$
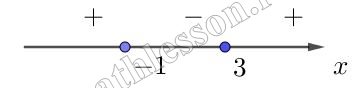
Отметим полученные точки на координатной прямой и расставим знаки выражения
Нам нужны неотрицательные значения $$\Rightarrow x\in (-\infty ;-1] \cup [3 ;+\infty ]$$, соответствует 2 варианту ответа.
Задание 4928
На каком рисунке изображено множество решений неравенства $$x^2 - 4x + 3 \ge 0$$?
1) $$( -\infty;\ 1 ] \cup [ 3;\ +\infty )$$
2) $$( -\infty;\ 1 ) \cup ( 3;\ +\infty )$$
3) $$[ 1;\ 3 ]$$
4) $$( 1;\ 3 )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Приравняем выражение слева к нулю: $$x^{2}-4x+3\geq 0 \Leftrightarrow$$$$x=1;3$$
Отметим полученные точки на координатной прямой (закрашенные, так как неравенство нестрогое).
Расставим знаки, которые принимает выражение на полученных промежутках (путем подстановки значений с этих промежутков в данное выражение):
Выберем те, где получен знак $$+$$. Тогда $$x \in (-\infty ;1]\cup [3;+\infty)$$, что соответствует 3 варианту ответа
Задание 4921
Задание 817
Решением какого из нижеследующих неравенств является отрезок $$[ -5;\ 5 ]$$?
1) $$x^2 + 25 \le 0$$
2) $$x^2 - 25 \le 0$$
3) $$x^2 + 25 \ge 0$$
4) $$x^2 - 25 \ge 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) $$x^25\leq0\Rightarrow x\in\varnothing$$ - нет
2) $$x^2-25\leq0\Rightarrow x\in [-5;5]$$ - да
3) $$x^2+25\geq0\Rightarrow x\in R$$ - нет
4) $$x^2-25\geq0\Rightarrow x\in (-\infty;-5]\cup[5;+\infty)$$ - нет
Задание 1351
Решите неравенство $$-x^2 + x \ge 0$$. В ответе укажите номер правильного варианта ответа:
1) $$( -\infty;\ 0 ) \cup ( 1;\ +\infty )$$
2) $$[ 0;\ 1 ]$$
3) $$( 0;\ 1 )$$
4) $$( -\infty;\ 0 ] \cup [ 1;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1220
Решите неравенство $$(2x - 5)(x + 3) \ge 0$$. В ответе укажите номер правильного варианта ответа:
1) $$( -\infty;\ -3 );\ ( \frac{5}{2};\ +\infty )$$
2) $$( -\infty;\ -3 ];\ [ \frac{5}{2};\ +\infty )$$
3) $$[ -3;\ -\frac{5}{2} ]$$
4) $$( -3;\ -\frac{5}{2} )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1755
Решите неравенство $$\sqrt{3x - 5} \ge 2x - 4$$. В ответе укажите номер правильного варианта ответа:
1) $$\left[\frac{5}{3};\ 3\right]$$
2) $$\left[\frac{7}{4};\ 3\right]$$
3) $$[ 3;\ +\infty )$$
4) $$( -\infty;\ 1 ] \cup \left[\frac{9}{5};\ +\infty\right)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4404
Решите неравенство $$4x^2 - (2x - 5)^2 \le 5(5x - 4)$$.
1) $$[ 1;\ +\infty )$$
2) $$[ -1;\ +\infty )$$
3) $$( -\infty;\ 1 ]$$
4) $$( -\infty;\ -1 ]$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$4x^{2}-(2x-5)^{2}\leq 5(5x-4)$$ $$4x^{2}-4x^{2}+20x-25-25x+20\leq 0$$ $$-5x-5\leq 0$$ $$\Leftrightarrow$$ $$-5x\leq 5$$ $$x\geq -1$$
Задание 4924
Решите неравенство $$x^2 361$$. В ответе укажите номер правильного варианта:
1) $$( -\infty;\ -19 ) \cup ( 19;\ +\infty )$$
2) $$( -\infty;\ -19 ] \cup [ 19;\ +\infty )$$
3) $$( -19;\ 19 )$$
4) $$[ -19;\ 19 ]$$
$$x^{2}<361 \Leftrightarrow$$$$(x-19)(x+19)<0 \Leftrightarrow$$$$\left\{\begin{matrix}x>-19\\x<19 \end{matrix}\right.$$ Что соответствует 3 варианту ответа (скобки круглые, так как неравенство строгое).
Задание 630
Решите неравенство: $$(x - 1)(3x - 5) 1$$
1) $$( -\infty;\ 1 ) \cup ( \frac{5}{3};\ +\infty )$$
2) $$( -\infty;\ \frac{2}{3} ) \cup ( 2;\ +\infty )$$
3) $$( \frac{2}{3};\ 2 )$$
4) $$( 1;\ \frac{5}{3} )$$
$$(x - 1)(3x - 5) < 1$$
$$3x^2 - 5x - 3x + 5 < 1$$
$$3x^2 - 8x + 4 < 0$$
$$D = 64 - 4\cdot3\cdot3 = 64 - 48 = 16=4^2$$
$$x_1 = \frac{8 + 4}{6} = 2$$
$$x_2 = \frac{8 - 4}{6} = \frac{2}{3}$$
Чертим промежуток: ___+___2/3___-___2___+___.
Выбираем тот, что меньше нуля $$\Rightarrow (\frac{2}{3};2)\Rightarrow3$$
Задание 3227
Укажите неравенство, которое не имеет решений:
1) $$x^2 - 6x - 15 > 0$$
2) $$x^2 - 6x + 15 0$$
3) $$x^2 - 6x - 15 0$$
4) $$x^2 - 6x + 15 > 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- $$x^{2}-6x-15=0\Leftrightarrow$$ $$D=36+4*15=96>0\Rightarrow$$ решение есть и для $$>0$$ и для $$<0$$.
- $$x^{2}-6x+15=0\Leftrightarrow$$ $$D=36-4*15<0\Rightarrow$$ т.к. $$a>0$$, то $$x^{2}-6x+15>0$$ при всех $$x\Rightarrow$$ не имеет решения $$x^{2}-6x+15<0$$, что соответсвует 2 варианту ответа
Задание 4923
Укажите неравенство, которое не имеет решений. В ответе укажите номер правильного варианта:
1) $$x^2 - 64 \le 0$$
2) $$x^2 + 64 \ge 0$$
3) $$x^2 - 64 \ge 0$$
4) $$x^2 + 64 \le 0$$
$$x^{2}+64\leq0$$, так как $$x^{2}$$ - число неотрицательное, к нему прибавляется положительное число. В результате получим однозначно положительное. А в неравенстве ищется отрицательное значение данного выражения, которое не существует.
Задание 3203
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


- $$x^{2}-36<0\Leftrightarrow$$ $$(x-6)(x+6)<0\Leftrightarrow$$ \left\{\begin{matrix}x>-6\\x<6\end{matrix}\right.$$
- $$x^{2}-6x>0\Leftrightarrow$$ $$x(x-6)>0\Leftrightarrow$$ $$\left\{\begin{matrix}x<0\\x>6\end{matrix}\right.$$
- $$x^{2}-6x<0\Leftrightarrow$$ $$x(x-6)<0\Leftrightarrow$$ $$\left\{\begin{matrix}x>0\\x<6\end{matrix}\right.$$
Следовательно, третий вариант ответа.
Задание 1695
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!