ОГЭ 2021. Вариант 7. Ященко 36 вариантов ФИПИ школе.
Решаем 7 вариант ОГЭ Ященко 2021 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 7 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1-5
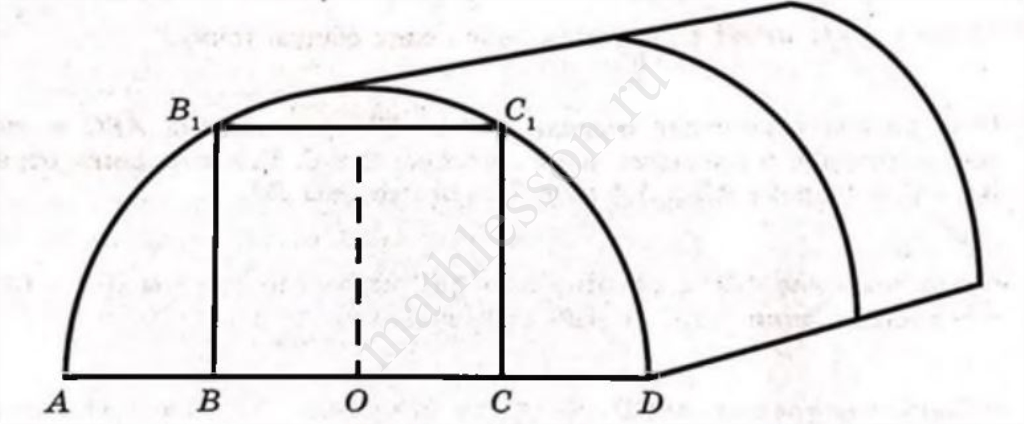
Теплицы
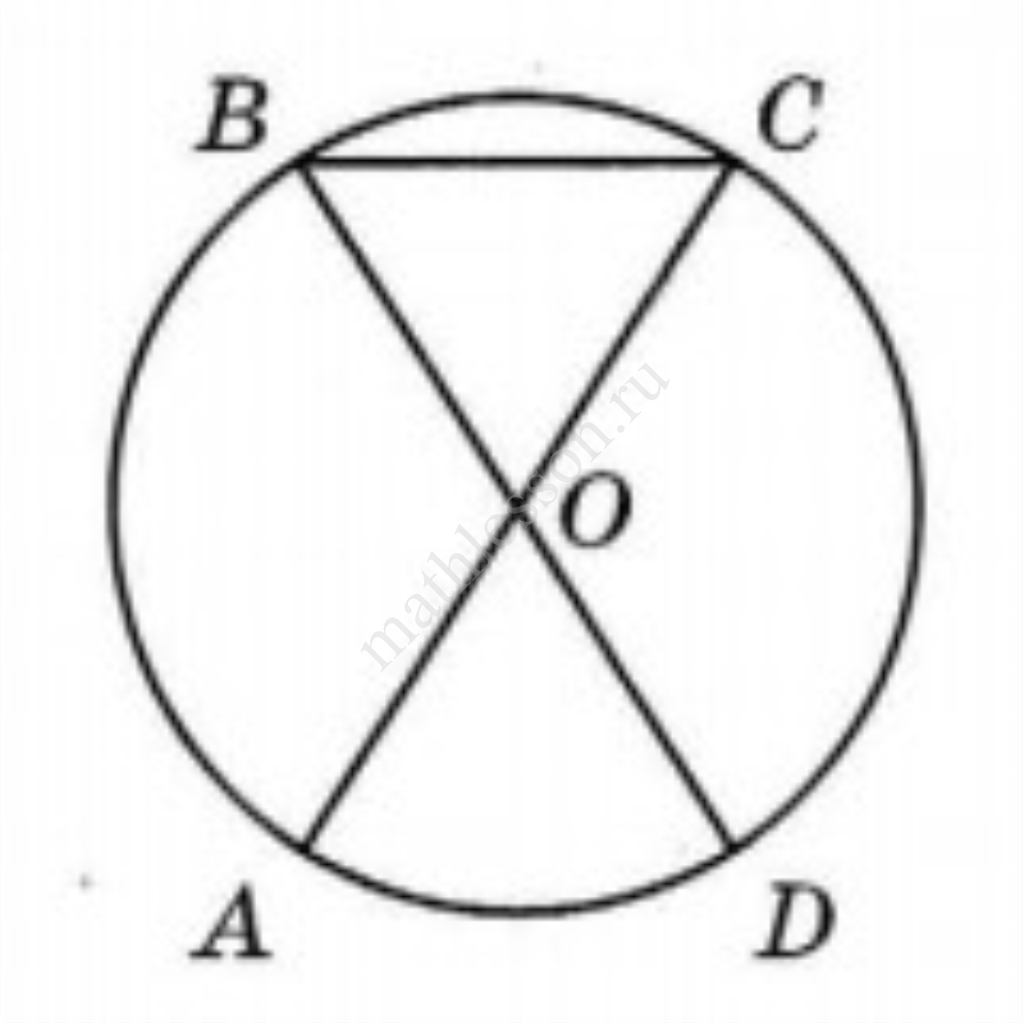
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки В, О и С делят отрезок АО на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
1. Какое количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 6
Задание 7
На координатной прямой отмечены числа $$x$$, $$y$$ и $$z$$. Какая из разностей $$x-y$$, $$y-z$$, $$z-x$$ положительна?
1) $$x - y$$
2) $$y - z$$
3) $$z - x$$
4) ни одна из них
Учтем, что в порядке возрастания числа расположатся следующим образом: $$z,x,y$$. Тогда:
- x-y<0
- y-z>0
- z-x<0
- ни одна из них
Как видим, положительным будет только второй вариант ответа
Задание 8
Найдите значение выражения $$\frac{3^{-7} \cdot 3^2}{3^{-9}}$$
Задание 9
Решите уравнение: $$x^2 - 20 = x$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
$$x^{2}-20=x\Leftrightarrow$$$$x^{2}-x-20=0$$
По теореме Виетта сумма корней равна 1, произведение -20. Следовательно, корни равны 5 и -4. В ответ необходимо указать больший, то есть 5
Задание 10
Вероятность того, что новый фен прослужит больше года, равна $$0,98$$. Вероятность того, что он прослужит больше двух лет, равна $$0,86$$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Задание 11
На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между графиками функций и знаками коэффициентов $$a$$ и $$c$$.
Коэффициенты
1. $$a > 0$$, $$c > 0$$
2. $$a > 0$$, $$c < 0$$
3. $$a < 0$$, $$c > 0$$
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Коэффициент а отвечает за направление ветвей параболы и расширение/сужение графика относительно оси Оу (если а>0 - ветви вверх, а<0 - вниз).
Коэффициент с за пересечение оси Оу графиком функции (если с>0, то пересечение над осью Ох, с<0 - под осью)
Тогда получим:
Задание 12
Работа постоянного тока (в джоулях) вычисляется по формуле $$A = \frac{U^2 t}{R}$$, где $$U$$ — напряжение (в вольтах), $$R$$ — сопротивление (в омах), $$t$$ — время (в секундах). Пользуясь этой формулой, найдите $$A$$ (в джоулях), если $$t = 9$$ с, $$U = 8$$ В и $$R = 12$$ Ом.
Подставим значения с условия задания: $$A=\frac{U^{2}t}{R}=\frac{8^{2}\cdot 9}{12}=48$$
Задание 13
Укажите решение неравенства: $$-3 - 5x \le x + 3$$
1) $$( -\infty;\ 0 ]$$
2) $$[ -1;\ +\infty )$$
3) $$[ 0;\ +\infty )$$
4) $$( -\infty;\ -1 ]$$
Задание 14
В $$11:00$$ часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В $$21:00$$ того же дня часы отставали на $$20$$ минут. На сколько минут отставали часы спустя $$24$$ часа после того, как они сломались?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 14$$, $$AB = 20$$. Найдите $$\sin B$$.
Задание 16
Отрезки $$AC$$ и $$BD$$ — диаметры окружности с центром $$O$$. Угол $$ACB$$ равен $$63^\circ$$. Найдите угол $$AOD$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
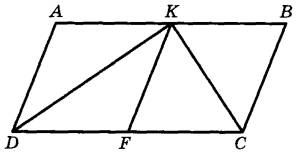
Площадь параллелограмма $$ABCD$$ равна $$92$$. Точка $$E$$ — середина стороны $$AB$$. Найдите площадь трапеции $$DAEC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 18
На клетчатой бумаге с размером клетки $$1 \times 1$$ изображён треугольник $$ABC$$. Найдите длину его медианы, проведённой из вершины $$C$$.
Задание 19
Какие из следующих утверждений верны?
- Площадь треугольника меньше произведения двух его сторон.
- Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
- Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
- Верно, так как по формуле она равна половине произведения двух смежных сторон на синус угла между ними, а синус угла всегда не больше единицы
- Нет, равен его половине
- Верно, и при том только одну
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) Перенесём всё в одну часть и применим формулу разности квадратов: $$x^4 - (2x - 3)^2 = 0,$$ $$(x^2 - (2x - 3))(x^2 + (2x - 3)) = 0,$$ $$(x^2 - 2x + 3)(x^2 + 2x - 3) = 0.$$
2) Решим квадратные уравнения.
Уравнение $$x^2 - 2x + 3 = 0.$$ Дискриминант: $$D = (-2)^2 - 4\cdot 1\cdot 3 = 4 - 12 = -8.$$ Действительных корней нет.
Уравнение $$x^2 + 2x - 3 = 0.$$ Дискриминант: $$D = 2^2 - 4\cdot 1\cdot(-3) = 4 + 12 = 16.$$ Корни: $$x_{1,2} = \dfrac{-2 \pm \sqrt{16}}{2\cdot 1} = \dfrac{-2 \pm 4}{2},$$ $$x_1 = 1,\quad x_2 = -3.$$
Задание 21
Моторная лодка прошла против течения реки $$132$$ км и вернулась в пункт отправления, затратив на обратный путь на $$5$$ часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна $$5$$ км/ч.
Пусть скорость лодки х км/ч. Тогда скорость против течения будет х-5 км/ч. а по течению х+5 км/ч
По условию на обратный путь затрачено на 5 часов меньше, тогда: $$\frac{132}{x-5}-\frac{132}{x+5}=5$$
Приведем к общему знаменателю: $$\frac{132(x+5)-132(x-5)}{x^2-25}=5$$
Задание 22
Постройте график функции $$y = x^2 + 3x - 3|x + 2| + 2$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 23
Прямая пересекает стороны $$AB$$ и $$BC$$ треугольника $$ABC$$ в точках $$K$$ и $$N$$ соответственно. Известно, что $$AB=12$$, $$BC=15$$, $$AC=24$$, $$AK=7$$, $$CN=11$$. Найдите длину отрезка $$KN$$.
- ВК=АВ-АК=12-7=5
- ВN=ВС-ВN=15-11=4
- Рассмотрим треугольники АВС и КВN. Угол В общий АВ/ВN=BC/BK, т.к.12/4 =15/5 =3 Следовательно данные треугольники подобны по двум сторонам и углу между ними, причем коэффициент подобия равен 3.
- Поэтому и АС/КN =3, т.е. 24/КN =3, т.е. КN=8
Задание 24
Сторона $$AB$$ параллелограмма $$ABCD$$ вдвое больше стороны $$AD$$. Точка $$K$$ - середина стороны $$AB$$. Докажите, что $$DK$$ - биссектриса угла $$ADC$$.
Проведём FK параллельно AD (см. рисунок). Тогда AD = AK = KB. Следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD делит угол ADC пополам.
