Задание 1120

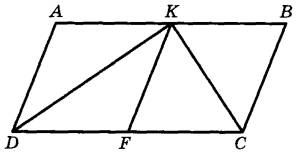
Сторона $$BC$$ параллелограмма $$ABCD$$ вдвое больше стороны $$CD$$. Точка $$L$$ - середина стороны $$BC$$. Докажите, что $$DL$$ - биссектриса угла $$ADC$$.

Сторона $$AD$$ параллелограмма $$ABCD$$ вдвое больше стороны $$CD$$. Точка $$M$$ - середина стороны $$AD$$. Докажите, что $$CM$$ - биссектриса угла $$BCD$$.

Сторона $$AB$$ параллелограмма $$ABCD$$ вдвое больше стороны $$AD$$. Точка $$K$$ - середина стороны $$AB$$. Докажите, что $$DK$$ - биссектриса угла $$ADC$$.

Сторона $$BC$$ параллелограмма $$ABCD$$ вдвое больше стороны $$CD$$. Точка $$K$$ - середина стороны $$BC$$. Докажите, что $$DK$$ - биссектриса угла $$ADC$$.

Сторона $$CD$$ параллелограмма $$ABCD$$ вдвое больше стороны $$BC$$. Точка $$N$$ - середина стороны $$CD$$. Докажите, что $$BN$$ - биссектриса угла $$ABC$$.

Сторона $$AB$$ параллелограмма $$ABCD$$ вдвое больше сторонь $$AD$$. Точка $$K$$ - середина стороны $$AB$$. Докажите, что $$DK$$ - биссектриса угла $$ADC$$.