Задание 2856
Задание 2856
Постройте график функции $$y = x^2 - 5x + 10 - 3|x - 2|$$ и определите, при каких значениях $$a$$ прямая $$y = a + 3$$ будет иметь с графиком три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Расскароем модуль:
$$\left\{\begin{matrix}x-2\geq 0\Rightarrow y=x^{2}+5x+10-3x+6\\x-2< 0\Rightarrow y=x^{2}+5x+10+3x-6\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}y=x^{2}-8x+16=(x-4)^{2},x\geq 0(1)\\y=x^{2}-2x+4, x<0(2)\end{matrix}\right.$$
В случае (1) дана парабола, ветви которой направлены вниз, получается она путем сдвига параболы вида $$y=x^{2}$$ на 4 единицы вправо по Ох.
В случае (2): найдем вершину: $$x_{0}=-\frac{-2}{2}=1$$, тогда $$y_{0}=1^{2}-2*1+4=3$$
Начертим оба графика:
Видим, что прямая $$y=a+3$$ будет иметь с графиком три общие точки в том случае, когда $$a+3=4\Leftrightarrow a=1$$ и $$a+3=3\Leftrightarrow a=0$$
Задание 1839
Постройте график функции $$y = x^2 + 11x - 4|x + 6| + 30$$. Определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком функции ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 2538
Постройте график функции $$y = x^2 - 7x - 5|x - 3| + 12$$. Найдите все значения $$m$$, при каждом из которых прямая $$y = m$$ имеет с графиком функции ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1122
Постройте график функции $$y = x^2 - 11x - 2|x - 5| + 30$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 1141
Постройте график функции $$y = x^2 + 3x - 3|x + 2| + 2$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 146
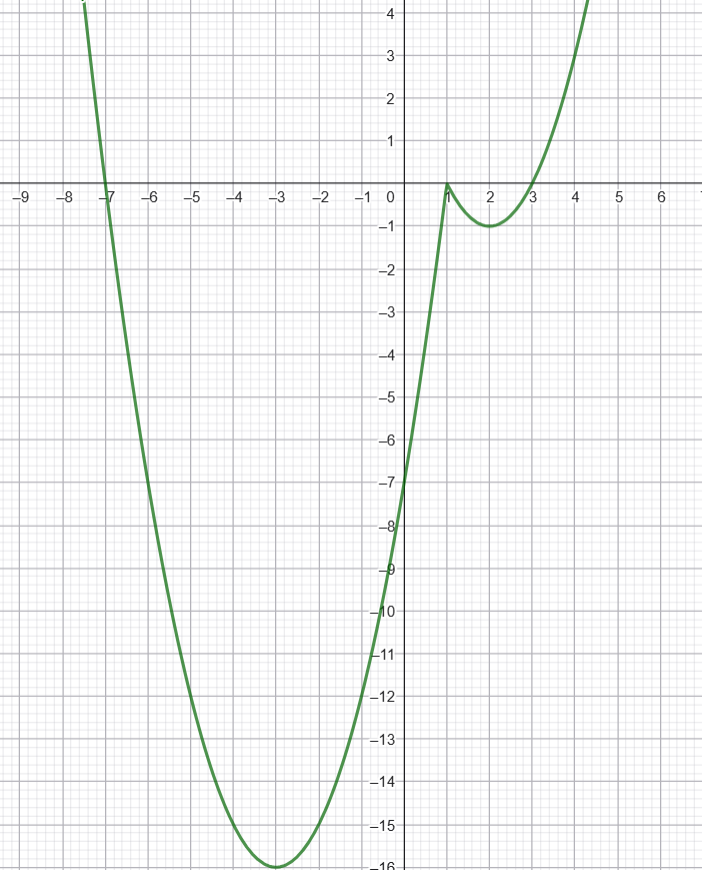
Постройте график функции $$y = x^2 + x - 5|x - 1| - 2$$. Определите, при каких значениях $$t$$ прямая $$y = t$$ имеет с графиком ровно три общие точки.
Рассмотрим два случая для модуля:
Случай 1: $$x \geq 1$$, тогда $$|x - 1| = x - 1$$
$$y = x^2 + x - 5(x - 1) - 2 = x^2 + x - 5x + 5 - 2 = x^2 - 4x + 3$$
Случай 2: $$x < 1$$, тогда $$|x - 1| = 1 - x$$
$$y = x^2 + x - 5(1 - x) - 2 = x^2 + x - 5 + 5x - 2 = x^2 + 6x - 7$$
В точке $$x = 1$$:
Слева: $$y = 1 + 6 - 7 = 0$$
Справа: $$y = 1 - 4 + 3 = 0$$
Функция непрерывна
Вершины парабол:
Для $$x \geq 1$$: $$x_0 = 2$$, $$y_0 = 4 - 8 + 3 = -1$$
Для $$x < 1$$: $$x_0 = -3$$, $$y_0 = 9 - 18 - 7 = -16$$
Прямая $$y = m$$ имеет 3 общие точки с графиком при:
$$m = 0$$ - точки: $$x = -7$$, $$x = 1$$, $$x = 3$$
$$m = -1$$ - точки: $$x = 2$$ (касание) и две другие
Задание 166
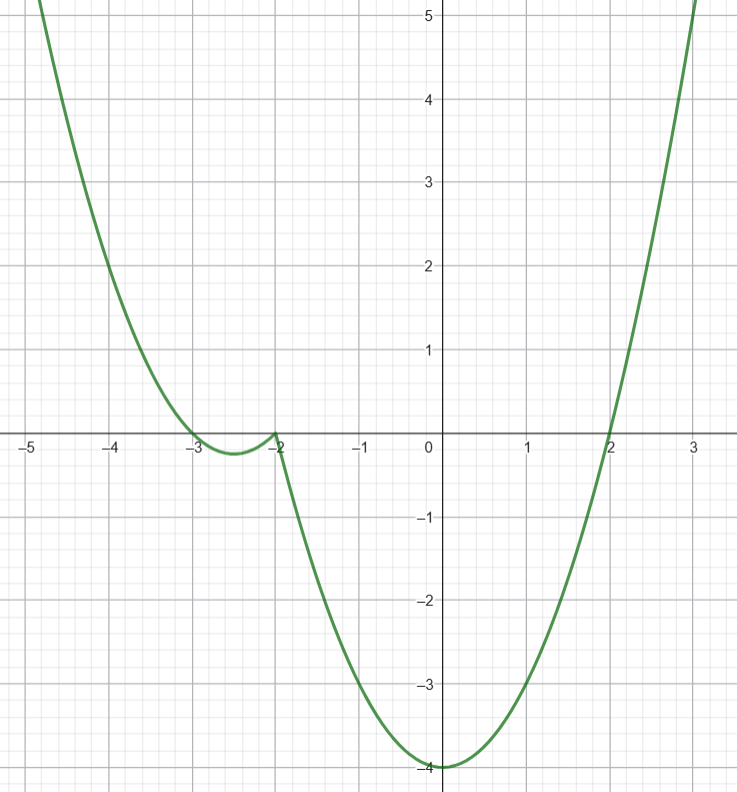
Постройте график функции $$y = x^2 + 2,5x - 2,5|x + 2| + 1$$. Определите, при каких значениях $$t$$ прямая $$y = t$$ имеет с графиком ровно три общие точки.
Решение:
Рассмотрим два случая для модуля:
Случай 1: $$x \geq -2$$, тогда $$|x + 2| = x + 2$$
$$y = x^2 + 2,5x - 2,5(x + 2) + 1 = x^2 + 2,5x - 2,5x - 5 + 1 = x^2 - 4$$
Случай 2: $$x < -2$$, тогда $$|x + 2| = -x - 2$$
$$y = x^2 + 2,5x - 2,5(-x - 2) + 1 = x^2 + 2,5x + 2,5x + 5 + 1 = x^2 + 5x + 6$$
$$y = (x + 2)(x + 3)$$
В точке $$x = -2$$:
Слева: $$y = 4 - 10 + 6 = 0$$
Справа: $$y = 4 - 4 = 0$$
Функция непрерывна
Вершины парабол:
Для $$x \geq -2$$: $$x_0 = 0$$, $$y_0 = -4$$
Для $$x < -2$$: $$x_0 = -2,5$$, $$y_0 = 6,25 - 12,5 + 6 = -0,25$$
Прямая $$y = m$$ имеет 3 общие точки с графиком при:
$$m = 0$$ - точки: $$x = -3$$, $$x = -2$$, $$x = 2$$
$$m = -0,25$$ - точки: $$x = -2,5$$ (касание) и две другие