ОГЭ 2021. Вариант 8. Ященко 36 вариантов ФИПИ школе.

Найдите значение выражения: $$\frac{1}{\frac{1}{21}+\frac{1}{28}}$$

На координатной прямой отмечены числа $$x$$, $$y$$ и $$z$$. Какая из разностей $$y - z$$, $$y - x$$, $$x - z$$ отрицательна?
1) $$y - z$$
2) $$y - x$$
3) $$x - z$$
4) ни одна из них

Найдите значение выражения $$\frac{2^{-6} \cdot 2^6}{2^{-8}}$$.

Решите уравнение: $$x^2 - 35 = 2x$$. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Вероятность того, что новый утюг прослужит больше года, равна $$0,94$$. Вероятность того, что он прослужит больше двух лет, равна $$0,85$$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

На рисунках изображены графики функций вида $$y = ax^2 + bx + c$$. Установите соответствие между графиками функций и знаками коэффициентов $$a$$ и $$c$$.

Коэффициенты:
1. $$a > 0$$, $$c < 0$$
2. $$a < 0$$, $$c > 0$$
3. $$a > 0$$, $$c > 0$$

ГРАФИКИ

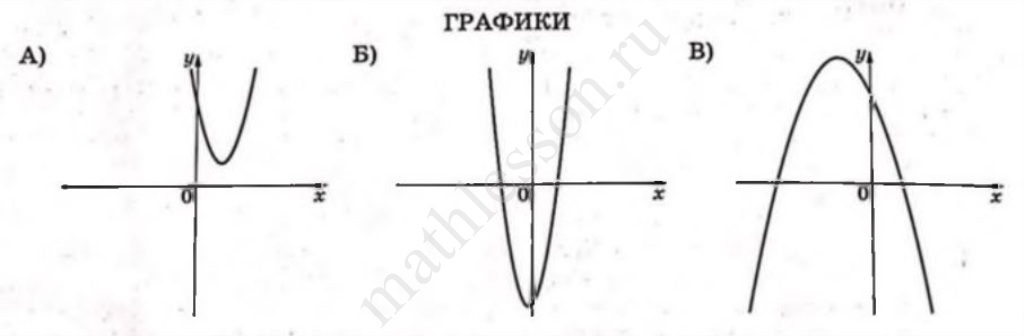
В таблице под каждой буквой укажите соответствующий номер.

Работа постоянного тока (в джоулях) вычисляется по формуле $$A = I^2 R t$$, где $$I$$ — сила тока (в амперах), $$R$$ — сопротивление (в омах), $$t$$ — время (в секундах). Пользуясь этой формулой, найдите $$A$$ (в джоулях), если $$t = 10$$ с, $$I = 4$$ А и $$R = 2$$ Ом.

Укажите решение неравенства: $$-3 - x 4x + 7$$
1) $$( -\infty;\ -0,8 )$$
2) $$( -2;\ +\infty )$$
3) $$( -\infty;\ -2 )$$
4) $$( -0,8;\ +\infty )$$

В $$8:00$$ часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В $$23:00$$ того же дня часы отставали на $$15$$ минут. На сколько минут отставали часы спустя $$36$$ часов после того, как они сломались?

В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 14$$, $$AB = 20$$. Найдите $$\sin B$$.

В окружности с центром $$O$$ отрезки $$AC$$ и $$BD$$ — диаметры. Угол $$AOD$$ равен $$108^\circ$$. Найдите угол $$ACB$$. Ответ дайте в градусах.

Две стороны параллелограмма равны $$10$$ и $$12$$, а один из углов этого параллелограмма равен $$30^\circ$$. Найдите площадь этого параллелограмма.

На клетчатой бумаге с размером клетки $$1 \times 1$$ изображен треугольник $$ABC$$. Найдите длину его медианы, проведённой из вершины $$C$$.

Какие из следующих утверждений верны:

1. Если диагонали параллелограмма равны, то он является ромбом.
2. Сумма острых углов прямоугольного треугольника равна 90 градусам.
3. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решите уравнение: $$x^4 = (3x - 4)^2$$

Постройте график функции $$y = x^2 - 11x - 2|x - 5| + 30$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно три общие точки.

Прямая пересекает стороны $$AB$$ и $$BC$$ треугольника $$ABC$$ в точках $$K$$ и $$N$$ соответственно. Известно, что $$AB=9$$, $$BC=12$$, $$AC=18$$, $$AK=5$$, $$CN=9$$. Найдите длину отрезка $$KN$$.

Сторона $$AD$$ параллелограмма $$ABCD$$ вдвое больше стороны $$AB$$. Точка $$G$$ — середина стороны $$AD$$. Докажите, что $$BG$$ — биссектриса угла $$ABC$$.

В трапеции $$ABCD$$ основания $$AD$$ и $$BC$$ равны соответственно $$34$$ и $$2$$, а сумма углов при основании $$AD$$ равна $$90^{\circ}$$. Найдите радиус окружности, проходящей через точки $$A$$ и $$B$$ и касающейся прямой $$CD$$, если $$AB=24$$.