ОГЭ 2026. Вариант 1 Ященко 36 вариантов ФИПИ школе.
Решаем 1 вариант ОГЭ Ященко 2026 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 1 варианта (всех заданий) Ященко 2026 ФИПИ 36 вариантов.
Рутуб
Ютуб
Задания:
Задание 1-5
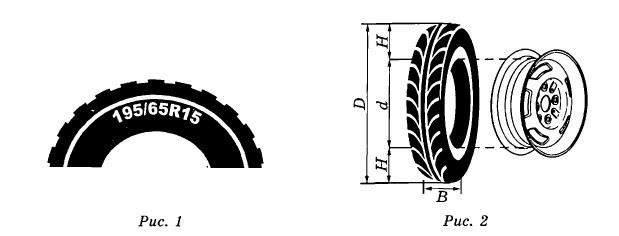
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
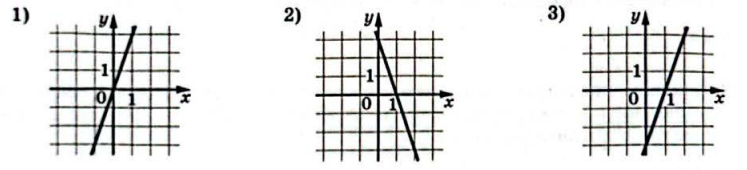
Для маркировки автомобильных шин применяется единая система обозначений. Например, $$195/65 R15$$ (рис. 1). Первое число обозначает дирину шины в миллиметрах (параметр $$B$$ на рисунке 2). Второе число - высота боковины шина $$H$$ в процентах от ширины шины. Например, шина с маркировкой $$195/65 R15$$ имеет ширину $$B = 195$$ мм и высоту боковины $$H = 195 \cdot 0,65 = 126,75$$ мм.
Буква $$R$$ означает, что шина имеет радиальную конструкцию, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. Такие шины применяются на всех легковых автомобилях.
За буквой $$R$$ следует диаметр диска $$d$$ в дюймах (в одном дюйме $$25,4$$ мм). Таким образом, общий диаметр колеса $$D$$ легко найти, зная диаметр диска и высоту боковины.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки $$215/50 R17$$.
1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм)/Диаметр диска (дюймы) | 16 | 17 | 18 |
| 205 | 205/60 | 205/55 | - |
| 215 | 215/60; 215/55 | 215/50 | 215/45 |
| 225 | - | 225/45; 225/40 | 225/40 |
1. Шины какой наибольшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен $$16$$ дюймам? Ответ дайте в миллиметрах.
2. Сколько миллиметров составляет высота боковины шины, имеющей маркировку $$225/40 R18$$?
3. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
4. На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами $$205/60 R16$$?
5. На сколько процентов уменьшится пробег автомобиля при одном обороте колеса, если заменить колеса, установленные на заводе, колесами с шинами $$225/40 R18$$? Результат округлите до десятых.
1) Смотрим столбец, соответствующий диаметру $$16$$: Видим, что наибольшая ширина $$215$$
2) Найдем высоту боковины шины: $$H = 225 \cdot 0,4 = 90$$
3) Найдем высоту боковины шины: $$H = 215 \cdot 0,5 = 107,5$$
Найдем диаметр колеса, выходящего с завода: $$D = 107,5 \cdot 2 + 17,25 \cdot 4 = 215 + 431,8 = 646,8$$
4) Найдем диаметр нового колеса: $$D_1 = 205 \cdot 0,6 \cdot 2 + 25,4 \cdot 16 = 246 + 406,4 = 652,4$$
Найдем изменение диаметра: $$\Delta D = 652,4 - 646,8 = 5,6$$
5) Найдем диаметр нового колеса: $$D_1 = 225 \cdot 0,4 \cdot 2 + 25,4 \cdot 18 = 180 + 457,2 = 637,2$$
Найдем изменение диаметра: $$\Delta D = 646,8 - 637,2 = 9,6$$
При этом, длина окружности находится по формуле $$C=2\pi R=\pi d$$. То есть длина окружности прямо пропорциональна диаметру окружности. Следовательно, на сколько процентов меняется диаметр, на столько меняется и длина окружности, и, как следствие, пробег:
$$646,8 - 100\%$$
$$9,6 - x\% $$
$$x = \frac{9,6 \cdot 100}{646,8} \approx 1,48 \approx 1,5$$ - на столько процентов уменьшится
Задание 7
На координатной прямой точками $$A$$, $$B$$, $$C$$ и $$D$$ отмечены числа $$\sqrt{0,05}$$; $$-\sqrt{0,05}$$; $$\sqrt{0,07}$$; $$-\sqrt{0,4}$$. Какому числу соответствует точка $$B$$?
1) $$\sqrt{0,05}$$
2) $$-\sqrt{0,05}$$
3) $$\sqrt{0,7}$$
4) $$-\sqrt{0,4}$$
![]()
Расположим числа в порядке возрастания. Очевидно, что $$0,4 > 0,05 \Rightarrow -\sqrt{0,4} < -\sqrt{0,05}$$. При этом $$0,05 < 0,7 \Rightarrow \sqrt{0,05} < \sqrt{0,7}$$.
То есть в порядке возрастания числа расположатся: $$-\sqrt{0,4}$$; $$-\sqrt{0,05}$$; $$\sqrt{0,05}$$; $$\sqrt{0,7}$$.
Точка $$B$$ на прямой вторая, то есть соответствует числу $$-\sqrt{0,05}$$. Значит, правильный ответ под номером $$2$$.
Задание 9
Решите уравнение $$x^2 - 9 = 5x + 5$$. Если уравнение имеет больше одного корня, в ответ запишите больший из корней.
$$x^2 - 9 = 5x + 5$$
$$x^2 - 5x - 14 = 0$$
$$D = (-5)^2 - 4 \cdot 1 \cdot (-14) = 25 + 56 = 81$$
$$x_{1,2} = \frac{5 \pm \sqrt{81}}{2} = \frac{5 \pm 9}{2}$$
$$x_1 = \frac{5 + 9}{2} = 7, \quad x_2 = \frac{5 - 9}{2} = -2$$
Больший из корней равен $$7$$.
Задание 10
В среднем из каждых $$120$$ поступивших в продажу аккумуляторов $$114$$ аккумуляторов заряжены. Найдите вероятность того, что выбранный в магазине наудачу аккумулятор не заряжен.
$$n = 120$$ - общее количество аккумуляторов
$$m = 120 - 114 = 6$$ - количество неисправных аккумуляторов
$$P = \frac{m}{n} = \frac{6}{120} = 0,05$$ - вероятность выбрать неисправный аккумулятор
Анализ формул:
А) $$y = -3x + 2$$ - убывающая прямая ($$k = -3 < 0$$), пересекает ось $$Oy$$ в точке $$(0; 2)$$
Б) $$y = 3x$$ - возрастающая прямая ($$k = 3 > 0$$), проходит через начало координат $$(0; 0)$$
В) $$y = 3x - 3$$ - возрастающая прямая ($$k = 3 > 0$$), пересекает ось $$Oy$$ в точке $$(0; -3)$$
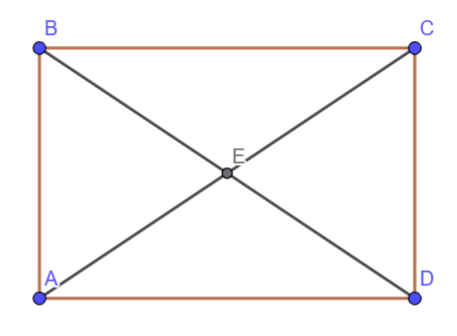
Анализ графиков:
График 1: убывающая прямая, пересекает ось y выше нуля → соответствует формуле А
График 2: возрастающая прямая, проходит через начало координат → соответствует формуле Б
График 3: возрастающая прямая, пересекает ось y ниже нуля → соответствует формуле В
Задание 12
Архимедова сила $$F$$ (в Н), действующая на погружённое в воду тело, вычисляется по формуле $$F = \rho g V$$, где $$\rho = 1000$$ кг/м3 — плотность воды, $$g = 9,8$$ м/с2 — ускорение свободного падения, а $$V$$ — объём тела в кубических метрах. Найдите архимедову силу, действующую на погружённое в воду тело объёмом $$0,05$$ куб. м. Ответ дайте в ньютонах.
Подставим в формулу $$F = \rho g V$$ известные значения:
$$F = 1000 \cdot 9,8 \cdot 0,05$$
$$F = 1000 \cdot 0,49$$
$$F = 490$$
Задание 13
Укажите решение неравенства $$(x + 8)(x - 5) > 0$$.
1) $$( -8;\ +\infty )$$
2) $$( 5;\ +\infty$$)
3) $$( -8;\ -5)$$
4) $$( -\infty;\ -8); ( 5;\ +\infty)$$
$$(x + 8)(x - 5) > 0$$
Пусть $$f(x)=(x + 8)(x - 5)$$
Пусть $$f(x)=0$$. Корни: $$x_1 = -8, \quad x_2 = 5$$
Метод интервалов:
Подставим в выражение $$f(x)$$ любое число $$x \in (-\infty; -8)$$. Например, $$x=-10$$. Тогда получим: $$(-10+8)(-10-5)=(-2)\cdot (-15) = 30 > 0$$ или $$\quad (-)(-) = (+) > 0$$
$$x \in (-8; 5): \quad (+)(-) = (-) < 0$$
$$x \in (5; +\infty): \quad (+)(+) = (+) > 0$$
Необходимо, чтобы $$f(x) > 0$$, то есть выбрать промежутки, где получили $$(+)$$.
Решение неравенства: $$x \in (-\infty; -8) \cup (5; +\infty)$$
Задание 14
Водитель автомобиля начал торможение. За секунду после начала торможения автомобиль проехал $$21$$ м, а за каждую следующую секунду он проезжал на $$3$$ м меньше, чем за предыдущую. Сколько метров автомобиль прошёл за первые $$5$$ секунд торможения?
Дано: $$a_1 = 21, \quad d = -3, \quad n = 5$$
Формула суммы: $$S_n = \frac{2a_1 + d(n-1)}{2} \cdot n$$
$$S_5 = \frac{2 \cdot 21 + (-3)(5-1)}{2} \cdot 5$$
$$S_5 = \frac{42 - 12}{2} \cdot 5$$
$$S_5 = \frac{30}{2} \cdot 5$$
$$S_5 = 15 \cdot 5 = 75$$
Задание 15
Сторона треугольника равна $$17$$, а высота, проведённая к этой стороне, равна $$14$$. Найдите площадь этого треугольника.
Формула площади треугольника: $$S = \frac{1}{2} a \cdot h$$, где $$a$$ - длина стороны, а $$h$$ - длина высоты, проведенной к этой стороне. Тогда:
$$S = \frac{1}{2} \cdot 17 \cdot 14 = 119$$
Задание 19
Какое из следующих утверждений является истинным высказыванием?
- Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники всегда равны.
- Существует прямоугольник, диагонали которого взаимно перпендикулярны.
- Угол, вписанный в окружность, всегда равен соответствующему центральному углу, опирающемуся на ту же дугу.
В ответе запишите номер выбранного утверждения.
- Нет. Такие треугольники называются подобными.
- Да. Такой прямоугольник называется квадратом ( да, квадрат - частный случай прямоугольника )
- Нет. Он равен половине соответствующего центрального угла.
Задание 20
Решите уравнение: $$2x^2 - 3x + \sqrt{2 - x} = \sqrt{2 - x} + 14$$
1) ОДЗ: $$2 - x \ge 0 \;\Rightarrow\; x \le 2.$$
2) Сократим одинаковые корни: $$2x^2 - 3x = 14,$$ $$2x^2 - 3x - 14 = 0.$$
3) Решим квадратное уравнение: $$D = (-3)^2 - 4\cdot 2\cdot(-14) = 9 + 112 = 121,$$ $$x_{1,2} = \dfrac{3 \pm \sqrt{121}}{4} = \dfrac{3 \pm 11}{4}.$$ Тогда $$x_1 = \dfrac{14}{4} = \dfrac{7}{2},\quad x_2 = \dfrac{-8}{4} = -2.$$ С учётом $$x \le 2$$ оставляем $$x = -2.$$
Задание 21
Автомобиль выехал с постоянной скоростью из города $$A$$ в город $$B$$, расстояние между которыми равно $$180$$ км. На следующий день он отправился обратно в $$A$$, увеличив скорость на $$5$$ км/ч, в результате чего затратил на обратный путь на $$24$$ минуты меньше. Найдите скорость автомобиля на пути из $$A$$ в $$B$$.
Пусть $$x > 0$$ - скорость из $$A$$ в $$B$$ (км/ч)
Тогда скорость обратно: $$x + 5$$ (км/ч)
Время из $$A$$ в $$B$$: $$t_1 = \frac{180}{x}$$
Время обратно: $$t_2 = \frac{180}{x + 5}$$
Разница во времени: $$24$$ мин = $$\frac{24}{60} = 0,4$$ ч
$$\frac{180}{x} - \frac{180}{x + 5} = 0,4$$
$$180(x + 5) - 180x = 0,4x(x + 5)$$
$$900 = 0,4x^2 + 2x$$
$$0,4x^2 + 2x - 900 = 0$$
Умножим на $$5$$: $$2x^2 + 10x - 4500 = 0$$
$$x^2 + 5x - 2250 = 0$$
$$D = 25 + 9000 = 9025$$
$$\sqrt{D} = 95$$
$$x_1 = \frac{-5 + 95}{2} = 45$$ - км/ч скорость из $$A$$ в $$B$$
$$x_2 = \frac{-5 - 95}{2} = -50 < 0$$
Задание 22
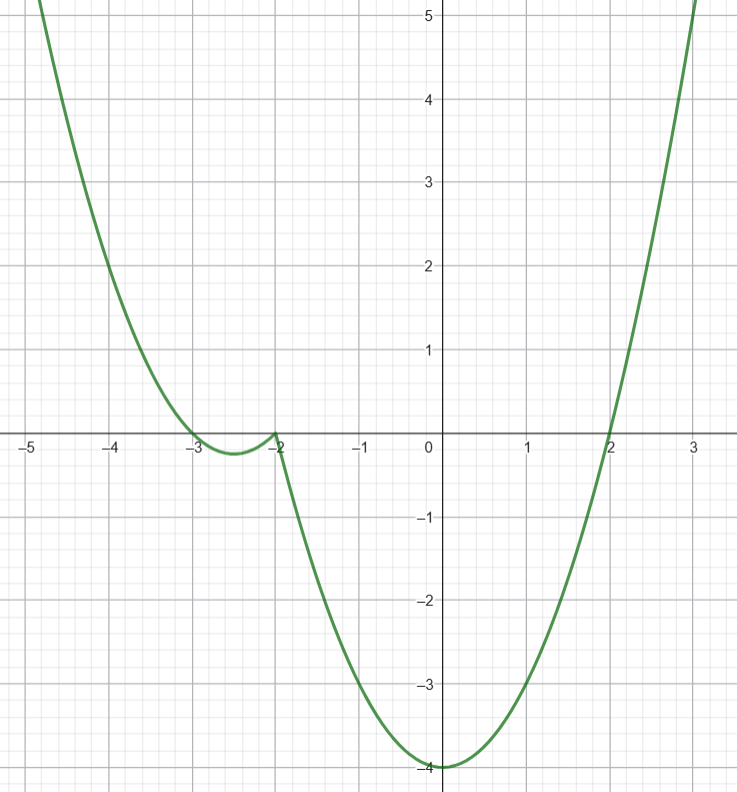
Постройте график функции $$y = x^2 + 2,5x - 2,5|x + 2| + 1$$. Определите, при каких значениях $$t$$ прямая $$y = t$$ имеет с графиком ровно три общие точки.
Решение:
Рассмотрим два случая для модуля:
Случай 1: $$x \geq -2$$, тогда $$|x + 2| = x + 2$$
$$y = x^2 + 2,5x - 2,5(x + 2) + 1 = x^2 + 2,5x - 2,5x - 5 + 1 = x^2 - 4$$
Случай 2: $$x < -2$$, тогда $$|x + 2| = -x - 2$$
$$y = x^2 + 2,5x - 2,5(-x - 2) + 1 = x^2 + 2,5x + 2,5x + 5 + 1 = x^2 + 5x + 6$$
$$y = (x + 2)(x + 3)$$
В точке $$x = -2$$:
Слева: $$y = 4 - 10 + 6 = 0$$
Справа: $$y = 4 - 4 = 0$$
Функция непрерывна
Вершины парабол:
Для $$x \geq -2$$: $$x_0 = 0$$, $$y_0 = -4$$
Для $$x < -2$$: $$x_0 = -2,5$$, $$y_0 = 6,25 - 12,5 + 6 = -0,25$$
Прямая $$y = m$$ имеет 3 общие точки с графиком при:
$$m = 0$$ - точки: $$x = -3$$, $$x = -2$$, $$x = 2$$
$$m = -0,25$$ - точки: $$x = -2,5$$ (касание) и две другие
Задание 23
Отрезки $$AB$$ и $$CD$$ являются хордами окружности. Найдите расстояние от центра окружности до хорды $$AB$$, если $$AB = 18$$, $$CD = 22$$, а расстояние от центра окружности до хорды $$CD$$ равно $$3$$.
Проведём из центра окружности $$O$$ перпендикуляры к хордам:
$$OH \perp AB$$, $$OK \perp CD$$
Тогда $$H$$ и $$K$$ - середины хорд
Для хорды $$CD$$:
$$CK = KD = \frac{CD}{2} = 11$$
$$OK = 3$$ (по условию)
Из треугольника $$OCK$$: $$OC^2 = OK^2 + CK^2 = 3^2 + 11^2 = 9 + 121 = 130$$
Для хорды $$AB$$:
$$AH = HB = \frac{AB}{2} = 9$$
$$OA = OC = R = \sqrt{130}$$
Из треугольника $$OAH$$: $$OH^2 = OA^2 - AH^2 = 130 - 81 = 49$$
$$OH = 7$$
Задание 24
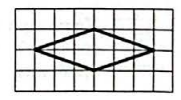
Внутри параллелограмма $$ABCD$$ выбрали произвольную точку $$E$$. Докажите, что сумма площадей треугольников $$AEB$$ и $$CED$$ равна половине площади параллелограмма.
Проведём через точку $$E$$ прямую $$MN \parallel AB$$
Площадь $$\triangle ABE = \frac{1}{2}S_{ABNM}$$ (*)
(*) Докажем это утверждение. Пусть $$EH$$ - высота в треугольнике $$ABE$$. Тогда $$S_{ABE} = \frac{1}{2} \cdot AB \cdot EH$$. Но $$S_{ABNM} = AB \cdot EH$$. Тогда $$S_{ABE}=\frac{1}{2}S_{ABNM}$$.Площадь $$\triangle CED = \frac{1}{2}S_{CNMD}$$
Сумма площадей: $$S_{ABE} + S_{CED} = \frac{1}{2}(S_{ABNM} + S_{CNMD})$$
Но $$S_{ABNM} + S_{CNMD} = S_{ABCD}$$
Таким образом: $$S_{ABE} + S_{CED} = \frac{1}{2}S_{ABCD}$$
Что и требовалось доказать.
Задание 25
Углы при одном из оснований трапеции равны $$36^\circ$$ и $$54^\circ$$, а отрезки, соединяющие середины противоположных сторон трапеции, равны $$25$$ и $$11$$. Найдите основания трапеции.
Пусть $$ABCD$$ - трапеция с основаниями $$AD$$ и $$BC$$
Обозначим середины сторон: $$M$$ - середина $$AB$$, $$N$$ - середина $$CD$$, $$P$$ - середина $$BC$$ - меньшее основание, $$Q$$ - середина $$AD$$ - большее основание трапеции.
Отрезки, соединяющие середины противоположных сторон:
$$MN$$ - средняя линия: $$MN = \frac{AD + BC}{2}$$
(*) Если сумма углов при основании трапеции равна $$90^\circ$$, то длина отрезка, соединяющего середины оснований, равна полуразности длин оснований. $$PQ = \frac{|AD - BC|}{2}$$
Решаем систему:
$$AD + BC = 50$$
$$AD - BC = 22$$
Сложим уравнения:
$$(AD + BC) + (AD - BC) = 50 + 22$$
$$2AD = 72$$
$$AD = 36$$
Вычтем уравнения:
$$(AD + BC) - (AD - BC) = 50 - 22$$
$$2BC = 28$$
$$BC = 14$$
$$AD = 36$$, $$BC = 14$$
Кому интересно, доказательство утверждения (*).
Пусть $$AB \cap DC = F$$. Угол $$\angle F = 90^\circ$$.
$$BP || AQ \Rightarrow \angle FBP = \angle FAQ$$ (соответственные).
$$FP$$ - медиана из прямого угла треугольник $$BFC \Rightarrow \angle BFP = \angle FBP$$, аналогично: $$\angle AFQ = \angle FAQ$$. Тогда $$\angle BFP = \angle AFQ \Rightarrow F, P, Q$$ лежат на одной прямой.
По свойству медианы, опущенной на гипотенузу: $$FP = \frac{BC}{2}$$, $$FQ = \frac{AD}{2}$$. При этом $$PQ = FQ - FP = \frac{AD}{2} - \frac{BC}{2} = \frac{AD - BC}{2}$$