Задание 1997
Задание 1997
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 4913
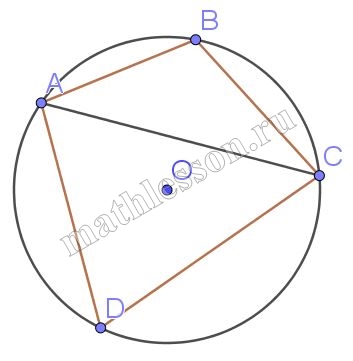
Четырёхугольник $$ABCD$$ вписан в окружность. Угол $$ABC = 136^\circ$$, угол $$CAD = 82^\circ$$. Найдите угол $$ABD$$. Ответ дайте в градусах.
Угол ABC - вписанный, следовательно, величина дуги ADC два раза больше (так как он опирается на данную дугу), тогда $$\smile ADC=272^{\circ}$$, аналогично $$\smile DC =2\angle CAD=164^{\circ}$$, тогда $$\smile AD=\smile ADC-\smile DC=272-164=108^{\circ}$$, но угол ABD опираются на эту дугу и является вписанным, следовательно, $$\angle ABD=\frac{1}{2}\smile AD=54^{\circ}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


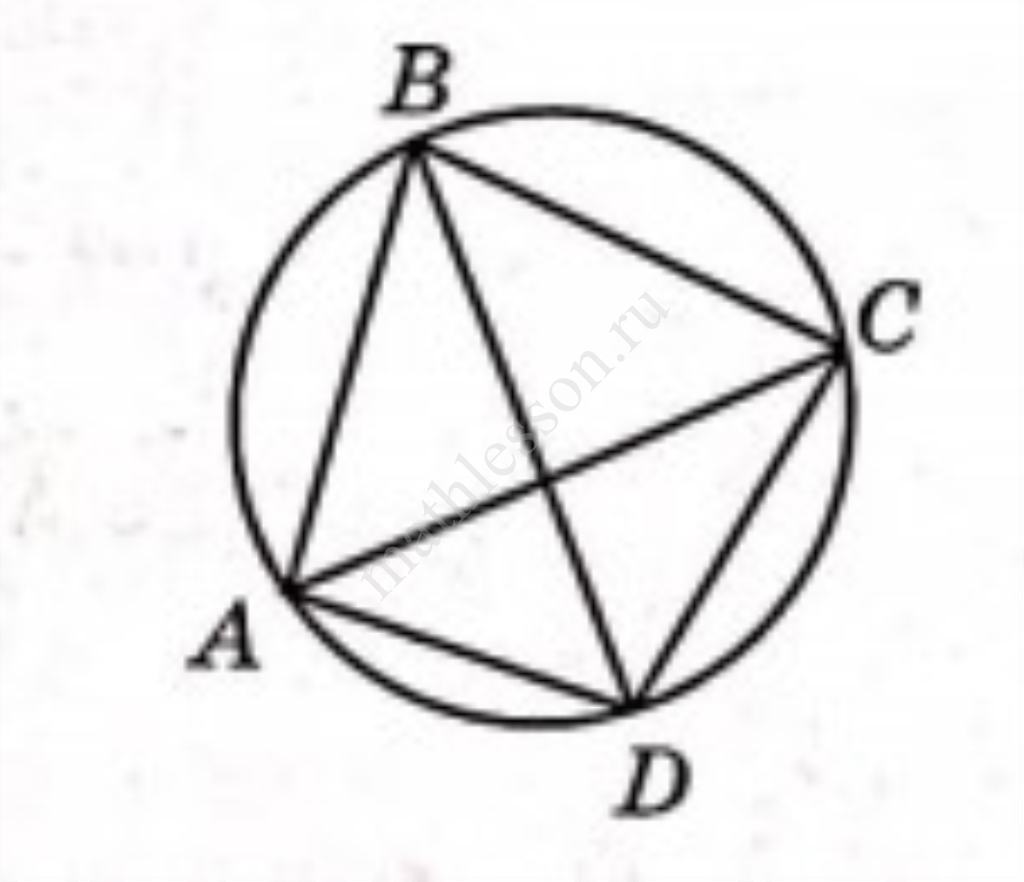
1) Вписанные углы, опирающиеся на одну дугу, равны:
$$\angle CAD = \angle CBD = 76^\circ$$
2) Угол $$ABC$$ состоит из двух углов:
$$\angle ABC = \angle ABD + \angle DBC$$
$$124^\circ = \angle ABD + 76^\circ$$
$$\angle ABD = 124^\circ - 76^\circ = 48^\circ$$