Задание 1978

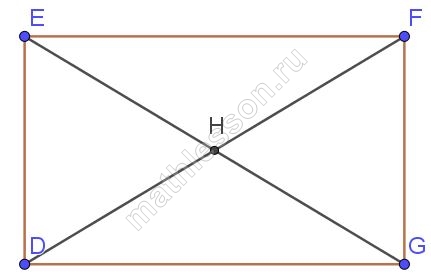
Пусть $$\angle EDH=51^{\circ}$$, по свойству диагоналей прямоугольника $$\angle DEH=\angle EDH$$, следовательно, из треугольника EHD по свойству суммы углов треугольника $$\angle EHD=180-2*51=78^{\circ}$$.

Причечание: при пересечении двух прямых получается две пары равных вертикальных углов, при нахождении угла между прямыми из них всегда выбирается острый, потому искать угол DHG нет смысла

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

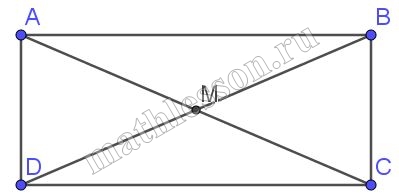
Пусть $$\angle CAB=36$$, тогда $$\angle ACB=180-36-36=108^{\circ}$$, и $$\angle ACD = 180-108=72^{\circ}$$. При пересечении двух прямых всегда берут острый угол.

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

1) пусть $$\angle OAD=48^{\circ}$$; по свойству прямоугольника: $$BD=AC ; AO=OC\Rightarrow \triangle AOD - $$ равнобедренный. тогда: $$ \angle ODA=\angle OAD$$

2)По свойству суммы углов в треугольнике: $$\angle AOD=180^{\circ}-(\angle OAD+\angle ODA)=$$$$180^{\circ}-2 \cdot 48^{\circ}=84^{\circ}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть $$\angle HDC=47^{\circ}$$, тогда $$\triangle HCD=47^{\circ}$$ (диагонали равны и точкой пересечения делятся пополам) $$\to$$ из $$\triangle DHC:\angle DHC=180-2\cdot 47=86^{\circ}$$

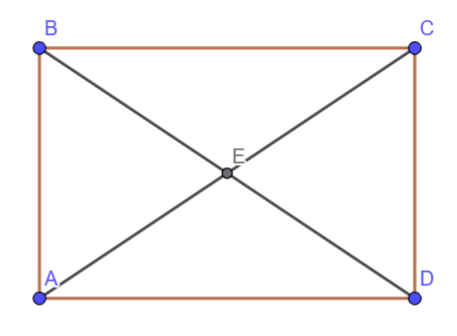
В прямоугольнике диагонали равны и точкой пересечения делятся пополам, то есть $$BE = AE$$. Пусть $$\angle BAE = 28^\circ$$. Тогда и $$\angle ABE = 28^\circ$$. Следовательно, $$\angle BEA = 180^\circ - 2 \cdot 28^\circ = 124^\circ$$

Тогда $$\angle AED = 180^\circ - \angle BEA = 56^\circ$$ (если просят найти угол между прямыми, то оказывается в ответ угол $$\leq 90^\circ$$, если не сказано иное)

В прямоугольнике диагонали равны и точкой пересечения делятся пополам, то есть $$BE = AE$$. Пусть $$\angle BAE = 68^\circ$$. Тогда и $$\angle ABE = 68^\circ$$. Следовательно, $$\angle BEA = 180^\circ - 2 \cdot 68^\circ = 44^\circ$$